Đề bài
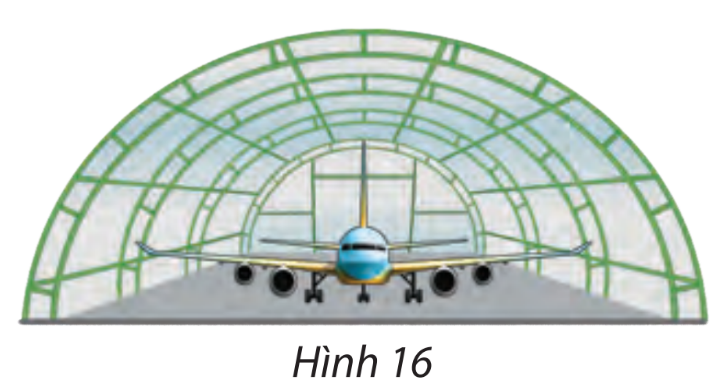
Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8 m, rộng 20 m (hình 16)
a) Chọn hệ tọa độ thích hợp và viết phương trình của elip nói trên
b) Tính khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm
Phương pháp giải - Xem chi tiết
a) Bước 1: Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm
Bước 2: Viết phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(M(x;y) \in (E);b = \sqrt {{a^2} - {c^2}} \)
b) Bước 1: Từ dữ kiện cách chân tường 5 m, xác định cách gốc tạo độ bao nhiêu (x=?)
Bước 2: Thay x vừa tìm được vào phương trình chính tắc tìm y
Lời giải chi tiết
a) Chọn hệ trục tọa độ Oxy với gốc tọa độ tại tâm đáy nhà vòm, trục tung thẳng đứng

Nhà vòm có dạng elip nên có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (với a,b>0)
Ta có chiều cao 8 m nên \(OA = h = 5\), chiều rộng của vòm là 20 m, suy ra \(BC = 2OB = 20 \Rightarrow OB = 10\)
Từ đó ta có tọa độ các điểm: \(C(10;0),A(0;5)\)
Thay hai điểm đó vào phương trinh chính tắc ta có:
\(\left\{ \begin{array}{l}\frac{{{{10}^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1\\\frac{{{0^2}}}{{{a^2}}} + \frac{{{5^2}}}{{{b^2}}} = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 10\\b = 5\end{array} \right.\)
Suy ra, phương trình miêu tả hình dáng nhà vòm là \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{25}} = 1\)
b) Điểm đó cách chân tưởng 5 m tương ứng cách tâm 5 m (vì từ tâm vòm đến tưởng là 10 m)
Thay \(x = 5\) vào phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{25}} = 1\), ta tìm được \(y = \frac{{5\sqrt 3 }}{2}\)
Vậy khoảng cách phương thẳng đứng từ một điểm cách chân tường 5 m đến nóc nhà vòm là \(\frac{{5\sqrt 3 }}{2}\) m
