Đề bài
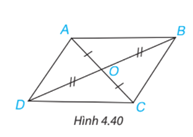
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau;
b) Chứng minh rằng \(\Delta \)DAB = \(\Delta \)BCD.
Phương pháp giải - Xem chi tiết
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
a) Xét \(\Delta AOB\) và \(\Delta COD\), có:
AO = CO (gt)
\(\widehat{AOB}=\widehat{COD}\) ( đối đỉnh)
OB = OD (gt)
\(\Rightarrow \Delta AOB = \Delta COD\) ( c.g.c)
Xét \(\Delta AOD\) và \(\Delta COB\), có:
AO = CO (gt)
\(\widehat{AOD}=\widehat{COB}\) ( đối đỉnh)
OD = OB (gt)
\(\Rightarrow \Delta AOD = \Delta COB\) ( c.g.c)
Vậy hai cặp tam giác có chung đỉnh O bằng nhau là: AOB và COD; AOD và COB theo trường hợp cạnh – góc – cạnh.
b)
Do \(\Delta AOD = \Delta COB\) nên: \(\widehat {ADO} = \widehat {CBO}\) (2 góc tương ứng) và AD=BC (2 cạnh tương ứng)
Xét \(\Delta DAB\) và \(\Delta BCD\), có:
AD=BC (cmt)
\(\widehat {ADO} = \widehat {CBO}\) (cmt)
BD chung
Vậy \(\Delta DAB =\Delta BCD\) (c.g.c)