Đề bài
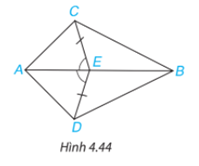
Cho Hình 4.44, biết \(EC = ED\) và \(\widehat {AEC} = \widehat {AED}\). Chứng minh rằng:
\(\begin{array}{*{20}{l}}{{\rm{ a) }}\Delta AEC = \Delta AED;}&{{\rm{ b) }}\Delta ABC = \Delta ABD.}\end{array}\)
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh.
Lời giải chi tiết
a)Xét hai tam giác AEC và AED có
\(EC = ED\)
\(\widehat {CEA} = \widehat {DEA}\)
AE chung
\( \Rightarrow \Delta AEC{\rm{ = }}\Delta AED\)(c.g.c)
b)
Do \(\Delta AEC{\rm{ = }}\Delta AED\) nên \(\widehat {CAE} = \widehat {DAE}\) ( 2 góc tương ứng) và AC=AD ( 2 cạnh tương ứng).
Xét \(\Delta ABC\) và \(\Delta ABD\) có:
AB chung
\(\widehat {CAE} = \widehat {DAE}\)
AC=AD
\( \Rightarrow \Delta ABC = \Delta ABD\)(c.g.c)