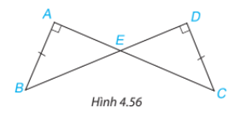
Đề bài
Cho hình 4.56, biết AB=CD, \(\widehat {BAC} = \widehat {BDC} = {90^o}\). Chứng minh rằng \(\Delta ABE = \Delta DCE\).
Phương pháp giải - Xem chi tiết
Chứng minh 2 tam giác vuông AEB và DEC bằng nhau theo trường hợp góc – cạnh - góc
Lời giải chi tiết
Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AEB và DEC có:
\(\widehat {AEB} = \widehat {DEC}\)(đối đỉnh) và \(\widehat {BAC} = \widehat {BDC} = {90^o}\).
Suy ra: \(\widehat {ABE} = \widehat {DCE}\)
Xét 2 tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {BDC} (= {90^o}\))
\(AB=DC\) (gt)
\(\widehat {ABE} = \widehat {DCE}\) (cmt)
=>\(\Delta AEB = \Delta DEC\)(g.c.g)