Đề bài
Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng \(\Delta ABC = \Delta DEF\). Hãy chứng minh AH = DK.
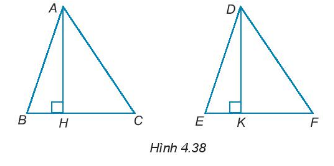
Phương pháp giải - Xem chi tiết
Chứng minh \(\Delta HAB = \Delta KDE\left( {ch - gn} \right)\)
Lời giải chi tiết
Ta có:
\(\begin{array}{l}\Delta ABC = \Delta DEF\\ \Rightarrow \left\{ \begin{array}{l}AB = DE\\\widehat {ABC} = \widehat {DEF} hay \widehat {HBA} = \widehat {KED}\end{array} \right.\end{array}\)
Xét \(\Delta HAB\) và \(\Delta KDE\) có:
\(\widehat {AHB} = \widehat {DKE} = {90^0}\\AB = DE\\\widehat {HBA} = \widehat {KED}\left( {cmt} \right)\\ \Rightarrow \Delta HAB = \Delta KDE\left( {ch - gn} \right)\)
\(\Rightarrow AH = DK\) (2 cạnh tương ứng)
