Đề bài
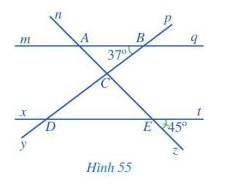
Quan sát Hình 55, trong đó mq // xt
a) Kể tên các cặp góc đồng vị bằng nhau.
b) Tìm số đo các góc BAC, CDE.
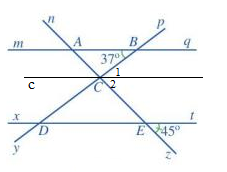
c) Bạn Nam cho rằng: Qua điểm C kẻ một đường thẳng c song song với hai đường thẳng mq và xt thì sẽ tính được \(\widehat {BCE} = 82^\circ \). Theo em, bạn Nam nói đúng hay sai? Vì sao?
Phương pháp giải - Xem chi tiết
+ 2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau
+ Sử dụng tính chất 2 đường thẳng song song: Nếu một đường thẳng cắt 2 đường thẳng song song thì 2 góc so le trong bằng nhau, 2 góc đồng vị bằng nhau.
+ Nếu tia Om nằm trong góc xOy thì \(\widehat {xOm} + \widehat {mOy} = \widehat {xOy}\)
Lời giải chi tiết
a) Các cặp góc đồng vị bằng nhau là: góc mAn và xEn; góc mAz và xEz; góc nAq và nEt; góc qAz và tEz; góc pBq và pDt; góc qBy và tDy; góc mBy và xDy; góc pBm và pDx
b) Vì mq // xt nên \(\widehat {BAC} = \widehat {zEt}\) ( 2 góc đồng vị) nên \(\widehat {BAC} = 45^\circ \).
Vì mq // xt nên \(\widehat {CDE} = \widehat {ABC}\) ( 2 góc so le trong) nên \(\widehat {CDE} = 37^\circ \).
c)
Bạn Nam nói đúng vì:
Vì c // mq nên \(\widehat {ABC} = \widehat {{C_1}}\) ( 2 góc so le trong) nên \(\widehat {{C_1}} = 37^\circ \)
Vì c // xt nên \(\widehat {CED} = \widehat {{C_2}}\) ( 2 góc so le trong) nên \(\widehat {{C_2}} = 45^\circ \)
Vì \(\widehat {{C_1}} + \widehat {{C_2}} = \widehat {BCE}\) nên \(\widehat {BCE} = \widehat {{C_1}} + \widehat {{C_2}} = 37^\circ + 45^\circ = 82^\circ \)