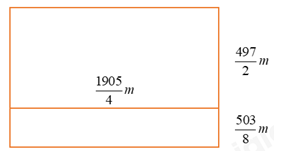
Đề bài
Hai thửa đất hình chữ nhật liền kề nhau có chung chiều dài là \(\frac{{1905}}{4}\)m còn chiều rộng lần lươt là \(\frac{{497}}{2}\)m và \(\frac{{503}}{8}\)m. Người ta gộp hai thửa đất trên thành một thửa đất cho thuận tiện sản xuất. Vẽ hình minh họa sơ đồ thửa đất sau khi gộp và tính diện tích của nó.
Phương pháp giải - Xem chi tiết
Vẽ hình minh họa gồm hai chữ nhật liền nhau có chung chiều dài.
Diện tích thửa đất sau khi gộp có 2 cách tính.
Lời giải chi tiết
Hình vẽ minh họa:
Cách 1:
Tổng hai chiều rộng của hai thửa đất là:
\(\frac{{497}}{2} + \frac{{503}}{8} = \frac{{2491}}{8}\left( m \right)\)
Vậy diện tích của cả thửa đất sau khi gộp là:
\(\frac{{1905}}{4}.\frac{{2491}}{8} = \frac{{4745355}}{{32}}\left( {{m^2}} \right)\)
Cách 2:
Diện tích của thửa đất thứ nhất là:
\(\frac{{1905}}{4}.\frac{{497}}{2} = \frac{{946785}}{8}\left( {{m^2}} \right)\)
Diện tích của thửa đất thứ hai là:
\(\frac{{1905}}{4}.\frac{{503}}{8} = \frac{{958215}}{{32}}\left( {{m^2}} \right)\)
Vậy diện tích của cả thửa đất là:
\(\frac{{946785}}{8} + \frac{{958215}}{{32}} = \frac{{4745355}}{{32}}\left( {{m^2}} \right)\)