Đề bài
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Lời giải chi tiết
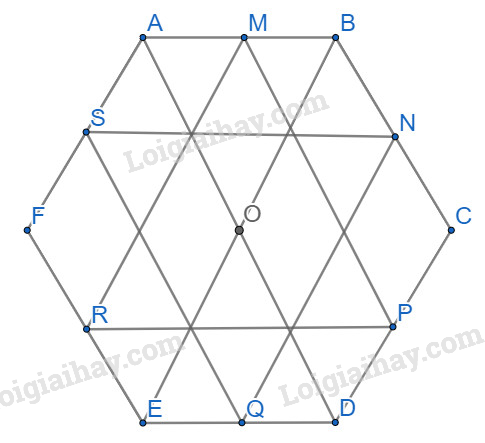
Gọi O là trọng tâm của tam giác MPR
Ta có MN là đường trung bình của tam giác ABC nên \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} \)
Tương tự PQ và RS cũng là đường trung bình của tam giác CDE và EFA nên
\(\overrightarrow {PQ} = \frac{1}{2}\overrightarrow {CE} ;\overrightarrow {RS} = \frac{1}{2}\overrightarrow {EA} \)
Từ đó suy ra \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \frac{1}{2}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {CE} + \frac{1}{2}\overrightarrow {EA} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right) = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0 \)
\( \Leftrightarrow \left( {\overrightarrow {MO} + \overrightarrow {ON} } \right) + \left( {\overrightarrow {PO} + \overrightarrow {OQ} } \right) + \left( {\overrightarrow {RO} + \overrightarrow {OS} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {ON} + \overrightarrow {OQ} + \overrightarrow {OS} = \overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} \)
Mà ta có O là trọng tâm của tam giác MPR nên \(\overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} = \overrightarrow 0 \)
Suy ra \(\overrightarrow {ON} + \overrightarrow {OQ} + \overrightarrow {OS} = \overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} = \overrightarrow 0 \)
Vậy O vừa trọng tâm của tam giác MPR vừa là trọng tâm của tam giác NQS
