Bài 5.1 phần bài tập bổ sung trang 119 SBT toán 9 tập 1

Đề bài

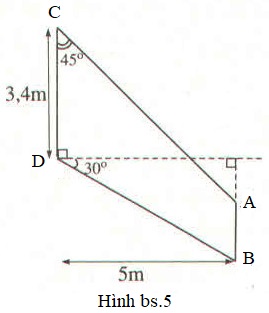
(h.bs. 5). Mô tả cánh của một máy bay. Hãy tính các độ dài \(AC,\; BD, \;AB\) của cánh máy bay theo số liệu được cho trong hình đó.

Lời giải chi tiết

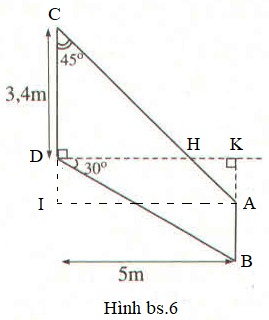
Đường thẳng \(AC\) cắt đường thẳng vuông góc với \(CD\) tại \(D\) ở điểm \(H\) thì tam giác \(CDH\) là tam giác vuông cân (vì là tam giác vuông có góc C bằng \(45^0\)), \(DH = CD = 3,4m\).

Đường thẳng \(AB\) cắt \(DH\) tại \(K\) thì \(DK = 5m\) nên \(H\) nằm ở giữa \(D\) và \(K\) (xem Hình bs.6).

Dựng hình chữ nhật \(AKDI\) thì \(AIC\) là tam giác vuông cân (vì là tam giác vuông có góc C bằng \(45^0\)), \(AI = KD = 5m\)

Xét tam giác vuông AIC ta có: \(AC = \sqrt {A{I^2} + I{C^2}}  = \sqrt {{5^2} + {5^2}}  = 5\sqrt 2\,(m) \)

Trong tam giác vuông \(BKD\), có:

\(\displaystyle DB = {{DK} \over {\cos 30^\circ }} = {5 \over {\displaystyle {{\sqrt 3 } \over 2}}} = {{10} \over {\sqrt 3 }} \) \(\displaystyle = {{10\sqrt 3 } \over 3} \approx 5,77\,(m)\)

Vì \(DC//AK\) (cùng vuông với DK) nên \(\widehat {KAH} = \widehat C = {45^0}\) (hai góc ở vị trí so le trong)

Suy ra \(HKA\) là tam giác vuông cân (tam giác vuông có góc A bằng \(45^0\))

Do đó: \(AK = HK = DK – DH = DK – DC\) \(= 5 – 3,4 = 1,6m\). 

Xét tam giác vuông BDK, ta có: \(KB = DK.tg30^\circ\) \(=5. \dfrac{\sqrt 3 }{3}\) \(= \dfrac{5\sqrt 3 }{3} \).  

Suy ra : \(AB = KB – KA\) \( \displaystyle = {{5\sqrt 3 } \over 3} - 1,6 \approx 1,29\,(m)\).

soanvan.me