Đề bài
Cho tam giác ABC vuông tại A, M là trung điểm của AC.
a) Vẽ E là hình chiếu của A trên đường thẳng BM.
b) Vẽ F là hình chiếu của C trên đường thẳng BM.
c) Chứng minh BE + BF > 2AB.
Phương pháp giải - Xem chi tiết
- Vẽ hình chiếu là vẽ đường vuông góc với chân đường vuông góc là hình chiếu.
- Sử dụng đường vuông góc và đường xiên để chứng minh BE + BF > 2AB
Lời giải chi tiết
a)
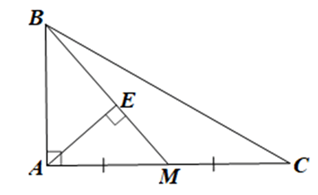
b)
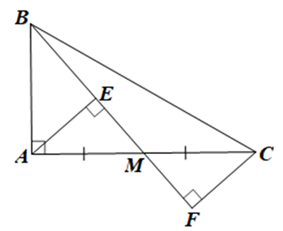
c) Xét ∆MAE và ∆MCF có:
\(\widehat {AEM} = \widehat {CFM}\left( { = 90^\circ } \right)\)
MA = MC (vì M là trung điểm của AC),
\(\widehat {AME} = \widehat {CMF}\) (hai góc đối đỉnh)
Do đó ∆MAE = ∆MCF (cạnh huyền – góc nhọn).
Suy ra ME = MF (hai cạnh tương ứng).
Ta có BA và BM lần lượt là đường vuông góc và đường xiên kẻ từ điểm B xuống đường thẳng AC
Suy ra AB < BM.
Hay AB < BE + EM (1) và AB < BF – MF (2)
Cộng vế theo vế của (1) và (2) ta có:
AB + AB < BE + EM + BF – MF
Mà ME = MF
Do đó 2AB < BE + BF.
Vậy BE + BF > 2AB.
