Tìm giá trị nguyên của biến \(x\) để tại đó giá trị của mỗi biểu thức sau là một số nguyên :
LG a
\(\displaystyle {2 \over {x - 3}}\)
Phương pháp giải:
- Tìm điều kiện xác định của các phân thức.
- Biến đổi biểu thức về dạng đơn giản.
- Để phân thức có giá trị là một số nguyên thì tử thức phải chia hết cho mẫu thức.
- Vận dụng kiến thức về ước đã học, tìm giá trị của \(x\).
Lời giải chi tiết:
\(\displaystyle {2 \over {x - 3}}\) là một số nguyên nên \(2 \vdots \left( {x - 3} \right)\) và \(x \ne 3\)
\(\Rightarrow x – 3 ∈ Ư(2) = \{ - 2; -1 ; 1; 2 \}\)
\(\eqalign{& x - 3 = - 2 \Rightarrow x = 1 (tm) \cr & x - 3 = - 1 \Rightarrow x = 2(tm) \cr & x - 3 = 1 \Rightarrow x = 4 (tm) \cr & x - 3 = 2 \Rightarrow x = 5(tm) \cr} \)
Vậy với \(x ∈ \{ 1; 2; 4; 5 \}\) thì \(\displaystyle {2 \over {x - 3}}\) là một số nguyên.
LG b
\(\displaystyle {3 \over {x + 2}}\)
Phương pháp giải:
- Tìm điều kiện xác định của các phân thức.
- Biến đổi biểu thức về dạng đơn giản.
- Để phân thức có giá trị là một số nguyên thì tử thức phải chia hết cho mẫu thức.
- Vận dụng kiến thức về ước đã học, tìm giá trị của \(x\).
Lời giải chi tiết:
\(\displaystyle {3 \over {x + 2}}\) là một số nguyên nên \(3 \vdots (x + 2)\) và \(x ≠ - 2\)
\(\Rightarrow x + 2 ∈ Ư(3) = \{ -3; -1; 1; 3 \}\)
\(\eqalign{ & x + 2 = - 3 \Rightarrow x = - 5 (tm) \cr & x + 2 = - 1 \Rightarrow x = - 3 (tm) \cr & x + 2 = 1 \Rightarrow x = - 1(tm) \cr & x + 2 = 3 \Rightarrow x = 1(tm) \cr} \)
Vậy với \(x ∈ \{ -5; -3; -1; 1 \}\) thì \(\displaystyle {3 \over {x + 2}}\) là một số nguyên
LG c
\(\displaystyle {{3{x^3} - 4{x^2} + x - 1} \over {x - 4}}\)
Phương pháp giải:
- Tìm điều kiện xác định của các phân thức.
- Biến đổi biểu thức về dạng đơn giản.
- Để phân thức có giá trị là một số nguyên thì tử thức phải chia hết cho mẫu thức.
- Vận dụng kiến thức về ước đã học, tìm giá trị của \(x\).
Lời giải chi tiết:
Đặt phép tính chia:
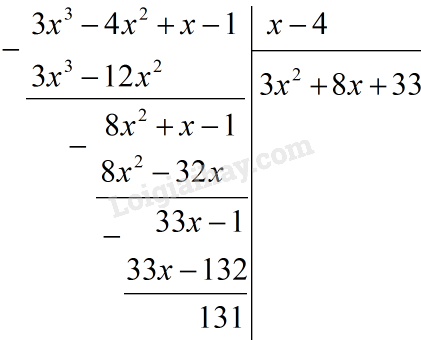
Từ phép chia trên ta có:
\(\displaystyle {{3{x^3} - 4{x^2} + x - 1} \over {x - 4}}\)\(\displaystyle = {{\left( {3{x^2} + 8x + 33} \right)\left( {x - 4} \right) + 131} \over {x - 4}}\)\(\displaystyle = 3{x^2} + 8x + 33 + {{131} \over {x - 4}}\)
Với \(x\) là số nguyên ta có : \(3{x^2} + 8x + 33\) là số nguyên
Vậy muốn biểu thức là số nguyên thì \(131 \vdots (x – 4 )\) và \(x ≠ 4\)
\(\Rightarrow x – 4 ∈ Ư(131) = \{-131; -1; 1;\)\( 131\}\)
\(\eqalign{ & x - 4 = - 131 \Rightarrow x = - 127(tm) \cr & x - 4 = - 1 \Rightarrow x = 3 (tm) \cr & x - 4 = 1 \Rightarrow x = 5 (tm)\cr & x - 4 = 131 \Rightarrow x = 135(tm) \cr} \)
Vậy \(x ∈ \{-127; 3; 5; 135\}\) thì \(\displaystyle {{3{x^3} - 4{x^2} + x - 1} \over {x - 4}}\) là số nguyên
LG d
\(\displaystyle {{3{x^2} - x + 1} \over {3x + 2}}\)
Phương pháp giải:
- Tìm điều kiện xác định của các phân thức.
- Biến đổi biểu thức về dạng đơn giản.
- Để phân thức có giá trị là một số nguyên thì tử thức phải chia hết cho mẫu thức.
- Vận dụng kiến thức về ước đã học, tìm giá trị của \(x\).
Lời giải chi tiết:
Ta có:
\(\displaystyle {{3{x^2} - x + 1} \over {3x + 2}}\)
\(\begin{array}{l}
= \dfrac{{3{x^2} + 2x - 3x - 2 + 3}}{{3x + 2}}\\
= \dfrac{{x\left( {3x + 2} \right) - \left( {3x + 2} \right) + 3}}{{3x + 2}}
\end{array}\)
\(\displaystyle = {{\left( {3x + 2} \right)\left( {x - 1} \right) + 3} \over {3x + 2}}\)\(\displaystyle = x - 1 + {3 \over {3x + 2}}\) (với \(x \ne \displaystyle - {3 \over 2}\) )
\(x\) là số nguyên nên \(x – 1\) là số nguyên.
Vậy muốn biểu thức đã cho là số nguyên thì \(3 ⋮ (3x + 2)\) và \(x \ne \displaystyle - {3 \over 2}\)
\(3x + 2 ∈ Ư(3) = \{-3; -1; 1; 3 \}\)
\(3x + 2 = - 3 \Rightarrow x = \displaystyle - {5 \over 3}\) (loại)
\(3x + 2 = - 1 \Rightarrow x = - 1(tm)\)
\(3x + 2 = 1 \Rightarrow x = \displaystyle - {1 \over 3} \) (loại)
\(3x + 2 = 3 \Rightarrow x = \displaystyle {1 \over 3} \) (loại)
Vậy với \(x = - 1\) thì biểu thức \(\displaystyle {{3{x^2} - x + 1} \over {3x + 2}}\) có giá trị nguyên.
soanvan.me
