Đề bài
Một khung dây thép hình chữ nhật có chiều dài 20 cm và chiều rộng 15 cm được uốn lại thành hình chữ nhật mới có kích thước \(\left( {20 + x} \right)\) cm và \(\left( {15 - x} \right)\) cm. Với x nằm trong các khoảng nào thì diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi?
Phương pháp giải - Xem chi tiết
Bước 1: Lập hiệu giữa diện tích mới và diện tích cũ \(f\left( x \right) = 20.15 - \left( {20 + x} \right)\left( {15 - x} \right)\) với \(x > 0\)
Bước 2: Tìm các khoảng thỏa mãn yêu cầu
+) Khoảng mà \(f\left( x \right) > 0\) là khoảng diện tích tăng lên
+) Khoảng mà \(f\left( x \right) < 0\) là khoảng diện tích giảm đi
+) Khoảng mà \(f\left( x \right) = 0\) là khoảng diện tích không đổi
Lời giải chi tiết
Theo giải thiết ta có tam thức sau: \(f\left( x \right) = 20.15 - \left( {20 + x} \right)\left( {15 - x} \right) = - {x^2} + 5x\)
Tam thức có \(\Delta = 25 > 0\), có hai nghiệm phân biệt \({x_1} = 0;{x_2} = 5\)
Ta có bảng xét dấu như sau
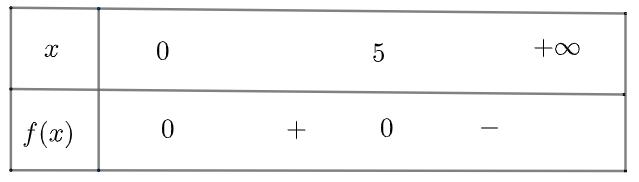
Vậy khoảng diện tích tăng lên là \(x \in \left( {0;5} \right)\), khoảng diện giảm đi là \(x > 5\) và diện tích không đổi khi \(x = 0\) và \(x = 5\)
Chú ý khi giải:
Vì x là độ dài nên điều kiện hiển nhiên của x là \(x > 0\)
