Đề bài
Cho hình thoi ABCD, biết AC là phân giác \(\widehat {BAD}\). Hãy chứng tỏ CA là phân giác \(\widehat {BCD}\).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình thoi có các cặp đối diện song song và bằng nhau. Sau khi đã chọn được cặp cạnh song song, ta sử dụng tính chất 2 góc so le trong bằng nhau để suy ra \(\widehat {DCA}\)=\(\widehat {ACB}\) nên CA là phân giác của \(\widehat {BCD}\)
Lời giải chi tiết
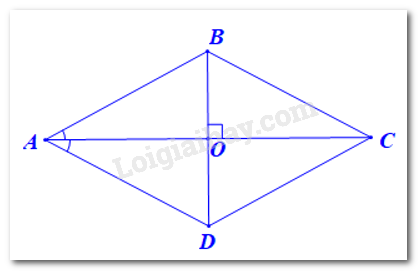
Vì ABCD là hình thoi nên AB // CD và AD // BC.
Do AB // CD nên \(\widehat {BAC}\)=\(\widehat {DCA}\) (hai góc so le trong)
Do AD // BC nên \(\widehat {CAD}\)=\(\widehat {ACB}\) (hai góc so le trong)
Mà AC là tia phân giác của \(\widehat {BAD}\) nên \(\widehat {BAC}\)=\(\widehat {CAD}\)
Suy ra \(\widehat {DCA}\)=\(\widehat {ACB}\)
Mà tia CA nằm giữa 2 tia CB và CD
Do đó CA là tia phân giác của \(\widehat {BCD}\)
