Đề bài
Lăng kính thủy tinh có tiết diện thẳng là tam giác cân ABC đỉnh A. Một tia sáng đơn sắc được chiếu vuông góc tới mặt bên AB. Sau hai lần phản xạ toàn phần trên hai mặt AC và AB, tia sáng ló ra khỏi đáy BC theo phương vuông góc với BC.
a) Vẽ đường truyền của tia sáng và tính góc chiết quang A.
b) Tìm điều kiện mà chiết suất n của lăng kính phải thỏa mãn.
Video hướng dẫn giải
Lời giải chi tiết
a) Vẽ đường truyền của tia sáng và tính góc chiết quang A.
+ Vẽ đường truyền của tia sáng ở hình 7
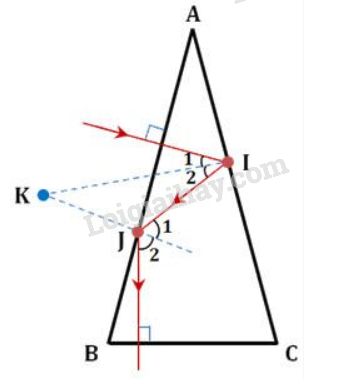
+ Tính góc chiết quang A.
Ta có: \(\widehat {{i_1}} = \widehat {{i_2}} = \widehat K = \widehat A\) (góc có cạnh tương ứng vuông góc)
=>Tam giác IJK cân tại J
Mặt khác\(\widehat {{J_1}} = \widehat B\) (góc có cạnh tương ứng vuông góc)
Áp dụng số đo góc ngoài của tam giác IJK :\(\widehat {{J_1}} = \widehat {{I_1}} + \widehat K = > \widehat B = 2\widehat A\)
Xét tam giác ABC có \(5\widehat A = {180^0} = > \widehat A = {36^0}\)
b) Tìm điều kiện mà chiết suất n phải thỏa mãn:\({i_1} \ge {i_{gh}}\)
Ta có \(i_{gh}=\widehat{A}={36^0}\)
Mặt khác:
\(sin{i_{gh}} = {\rm{ }}{1 \over n} >= sin{36^0} = 0,587785 = > n >= 1,7.\)
soanvan.me
