Đề bài
Trên mặt phẳng tọa độ (h.10), có một điểm \(M\) thuộc đồ thị của hàm số \(y = a{x^2}\).
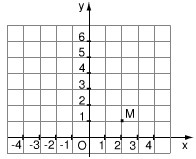
Hình 10
a) Tìm hệ số \(a\)
b) Điểm \(A(4; 4)\) có thuộc đồ thị không ?
c) Hãy tìm thêm hai điểm nữa (không kể điểm O) để vẽ đồ thị.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Điểm \(A(x_0; y_0)\) thuộc đồ thị hàm số. Thay \(x=x_0,\ y=y_0\) vào công thức hàm số \(y=ax^2\) ta tìm được \(a\).
b) Thay tọa độ điểm \(B(x_B; y_B)\) vào công thức hàm số \(y=ax^2\). Nếu ta được một đẳng thức đúng thì \(B\) thuộc đồ thị hàm số \(y=ax^2\).
c) Điểm \(A(x_0; y_0)\) có điểm đối xứng qua trục \(Oy\) là: \(A'(-x_0; y_0)\).
Lời giải chi tiết
a) Vì \(M(2;1)\) thuộc hàm số \(y=ax^2\), thay \(x=2,\ y=1\) vào công thức hàm số, ta có:
\(1=a.2^2 \Leftrightarrow 1=a.4 \Leftrightarrow a=\dfrac{1}{4}\)
Khi đó , hàm số đã cho có dạng là: \(y=\dfrac{1}{4}x^2\) (1).
b) Thay \(x=4,\ y=4\) vào công thức hàm số (1), ta được:
\(4=\dfrac{1}{4}.4^2 \) \(\Leftrightarrow 4=4\) (luôn đúng)
Vậy điểm \(A(4; 4)\) thuộc đồ thị hàm số \(y = \dfrac{1}{4}{x^2}\).
c) Ta có điểm \(A'(-4;4)\) đối xứng với điểm \(A(4; 4)\) qua trục tung
Điểm \(M'(-2; 1)\) đối xứng với điểm \(M(2; 1)\) qua trục tung
Vì đồ thị hàm số \(y=\dfrac{1}{4}x^2\) là đường cong đi qua gốc tọa độ, nhận trục \(Oy\) làm trục đối xứng nên \(A',\ M'\) cũng thuộc đồ thị.
Vẽ đồ thị:
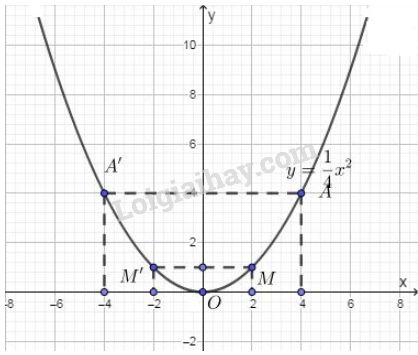
soanvan.me
