Cho hình chóp S.ABCD, đáy ABCD là tứ giác có hai đường chéo vuông góc với nhau tại H và SH là đường cao của hình chóp đã cho.
LG 1
Chứng minh rằng bốn tâm mặt cầu ngoại tiếp các hình chóp S.HAB, S.HBC, S.HCD, S.HDA là bốn đỉnh của một hình chữ nhật.
Lời giải chi tiết:
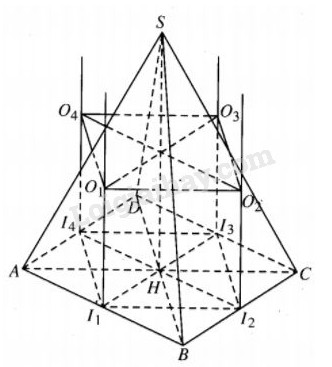
Gọi I1 là trung điểm của AB và O1 là tâm mặt cầu ngoại tiếp hình chóp S.ABH thì \({I_1}{O_1}// SH\) và \({I_1}{O_1} = {1 \over 2}SH.\)
Tương tự như trên, nếu \({I_2},{I_3},{I_4}\) thứ tự là trung điểm của BC, CD, DA và \({O_2},{O_3},{O_4}\) thứ tự là tâm của mặt cầu ngoại tiếp các hình chóp S.HBC, S.HCD, S.HDA thì
\(\eqalign{ & {I_2}{O_2} = {1 \over 2}SH,{I_3}{O_3} = {1 \over 2}SH, \cr & {I_4}{O_4} = {1 \over 2}SH, \cr} \)
và \({I_2}{O_2},{I_3}{O_3},{I_4}{O_4}\) cùng song song với SH.
Dễ thấy \({I_1}{I_2}//{O_1}{O_2}\) và \({I_1}{I_2}//AC,\)
\({I_2}{I_3}//{O_2}{O_3}\) và \({I_2}{I_3}//BD,\)
\({I_3}{I_4}//{O_3}{O_4}\) và \({I_3}{I_4}//AC,\)
\({I_4}{I_1}//{O_4}{O_1}\) và \({I_4}{I_1}//BD.\)
Kết hợp với \(AC \bot BD,\) ta có \({O_1}{O_2}{O_3}{O_4}\) là hình chữ nhật.
LG 2
Gọi H1, H2, H3, H4 là hình chiếu của H lần lượt trên AB, BC, CD, DA . Chứng minh rằng hình chóp S. H1H2H3H4 có mặt cầu ngoại tiếp. Tính diện tích của thiết diện của mặt cầu ấy khi cắt bởi mp(ABCD) nếu biết H1H3 =a,\(\widehat {BAC} = \alpha ,\widehat {BDC} = \beta \)
Lời giải chi tiết:
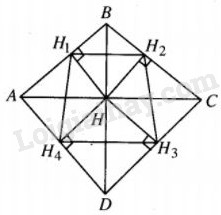
Dễ thấy \(\widehat {H{H_1}{H_2}} = \widehat {HB{H_2}} = \widehat {HBC},\)
\(\widehat {H{H_1}{H_4}} = \widehat {HA{H_4}} = \widehat {HAD},\)
\(\widehat {H{H_3}{H_2}} = \widehat {HC{H_2}} = \widehat {HCB},\)
\(\widehat {H{H_3}{H_4}} = \widehat {HD{H_4}} = \widehat {HDA}\)
Từ đó
\(\widehat {H{H_1}{H_2}} + \widehat {H{H_1}{H_4}} + \widehat {H{H_3}{H_2}} + \widehat {H{H_3}{H_4}}\)
\(= \widehat {HBC} + \widehat {HCB} + \widehat {HAD} + \widehat {HDA} = {180^0}\)
Vậy \({H_1}{H_2}{H_3}{H_4}\) là tứ giác nội tiếp đường tròn.
Từ đó hình chóp S. \({H_1}{H_2}{H_3}{H_4}\) có mặt cầu ngoại tiếp.
Diện tích thiết diện của hình cầu đó và mặt phẳng (ABCD) là diện tích hình tròn ngoại tiếp tứ giác \({H_1}{H_2}{H_3}{H_4}\).
Vì \(\widehat {BAC} = \alpha ,\widehat {BDC} = \beta \) nên \(\widehat {{H_1}{H_4}{H_3}} = \alpha + \beta \). Khi ấy \({{{H_1}{H_3}} \over {\sin (\alpha + \beta )}} = 2R\) (R là bán kính đường tròn ngoại tiếp tứ giác \({H_1}{H_2}{H_3}{H_4}\)), từ đó \(R = {a \over {2\sin (\alpha + \beta )}}.\)
Vậy diện tích hình thu được là
\(4\pi {R^2} = {{\pi {a^2}} \over {{{\sin }^2}(\alpha + \beta )}}.\)
soanvan.me
