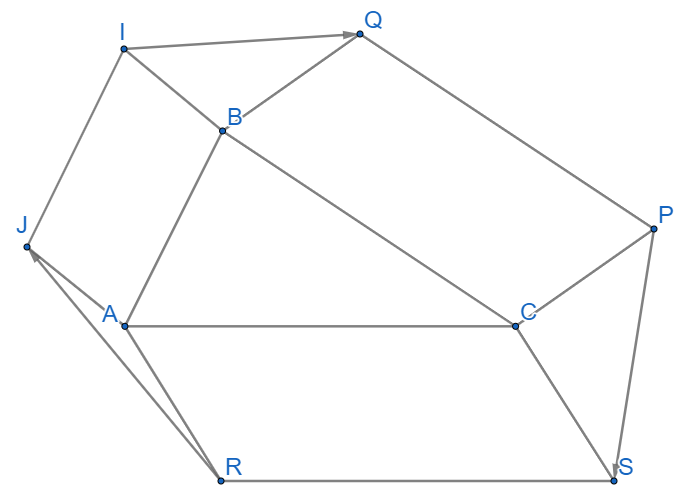
Đề bài
Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng \(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0 \).
Phương pháp giải - Xem chi tiết
Bước 1: Sử dụng quy tắc ba điểm \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} \)
Bước 2: Xác định các cặp vectơ đối nhau từ các hình bình hành \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) là hai vectơ đối nhau với ABCD là hình bình hành
Bước 3: Sử dụng tính chất của vectơ đối \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) là hai vectơ đối nhau thì\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow 0 \)
Lời giải chi tiết
\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)\)
\( = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)\(\)(đpcm)