Đề bài
Cho đường tròn (O) đường kính \(AB = 25cm,\) dây \(AC = 15cm.\) Vẽ dây CD vuông góc với AB tại H.
a) Tam giác ABC là tam giác gì ? Vì sao ?
b) Tam giác BCD là tam giác gì ? Vì sao ?
c) Tính các độ dài AH, CD.
Phương pháp giải - Xem chi tiết
a) Dùng định lí : Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
b) Chứng minh tam giác có đường cao cũng là đường trung tuyến.
c) Dùng hệ thức về cạnh và đường cao trong tam giác vuông : Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Lời giải chi tiết
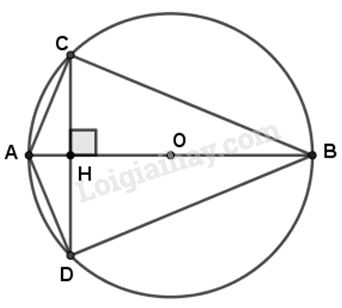
a) Tam giác \(ABC\) vuông tại \(C\) vì tam giác \(ABC\) có \(AB\) là đường kính của \(\left( O \right).\)
(tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông).
b) Đường kính \(AB\) vuông góc với \(CD\) nên \(CH = HD\) (Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây đó ).
Tam giác \(BCD\) có đường cao \(BH\) cũng là đường trung tuyến nên tam giác đó cân tại \(B.\)
c) Tam giác \(ABC\) vuông tại \(C,\) đường cao \(CH\) nên \(A{C^2} = AB.AH,\) tức là \({15^2} = 25.AH.\)
Suy ra \(AH = \dfrac{{225}}{{25}} = 9\left( {cm} \right).\)
Áp dụng định lí Py-ta-go vào tam giác vuông \(ACH,\) ta tính được
\(C{H^2} = A{C^2} - A{H^2} = {15^2} - {9^2} = 144\) nên \(CH = 12cm.\)
Suy ra \(CD = 2CH = 2.12 = 24\left( {cm} \right).\)
soanvan.me
