Đề bài
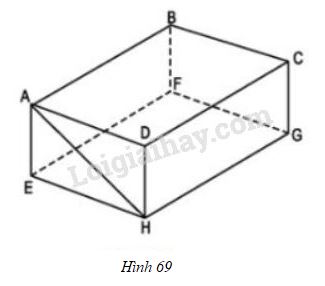
Hình hộp chữ nhật \(ABCD.EFGH\) (h69) có cạnh \(AB\) song song với mặt phẳng \((EFGH)\).
a) Hãy kể tên các cạnh khác song song với mặt phẳng \((EFGH)\)
b) Cạnh \(CD\) song song với những mặt phẳng nào của hình hộp chữ nhật?
c) Đường thẳng \(AH\) không song song với mặt phẳng \((EFGH)\), hãy chỉ ra mặt phẳng song song với đường thẳng đó.
Phương pháp giải - Xem chi tiết
Áp dụng các định nghĩa:
- Hình hộp chữ nhật.
- Khi đường thẳng \(d\) không nằm trong mặt phẳng \((ABCD)\) mà \(d\) song song với đường thẳng của mặt phẳng này thì ta nói đường thẳng \(d\) song song với mặt phẳng \((ABCD)\).
- Hình bình hành.
Lời giải chi tiết
a) Ta biết, \(6\) mặt của hình hộp chữ nhật đều là hình chữ nhật, do đó ta có:
\(BC//FG\) mà \(FG \subset mp\left( {EFGH} \right)\), suy ra \(BC//mp(EFGH)\)
\(AD//EH\) mà \(EH \subset mp\left( {EFGH} \right)\), suy ra \(AD//mp(EFGH)\)
\(DC//HG\) mà \(HG \subset mp\left( {EFGH} \right)\), suy ra \(DC//mp(EFGH)\)
b) \(CD//AB\) mà \(AB \subset mp\left( {ABFE} \right)\), suy ra \(CD//mp(ABFE)\)
\(CD//mp(EFGH)\) đã nói ở câu a)
Vậy \(CD\) song song với hai mặt phẳng \((ABFE)\) và \((EFGH)\).
c) Kẻ thêm đường chéo \(BG\) của hình chữ nhật \(BCGF\).
Xét tứ giác \(ABGH\), ta có:
\(AB=GH\) (vì cùng bằng \(CD\)) (1)
\(AH=BG\) (vì là đường chéo của hai hình chữ nhật bằng nhau) (2)
Từ (1) và (2) suy ra \(ABGH\) là hình bình hành, suy ra \(AH//BG\).
\(AH//BG\) mà \(BG \subset mp\left( {BCGF} \right)\), suy ra \(AH//mp\left( {BCGF} \right)\).
soanvan.me