Đề bài
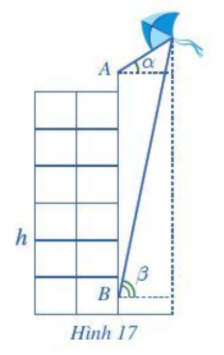
Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là \(\alpha = {35^o}\); khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1,5 m. Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là \(\beta = {75^o}\); khoảng cách từ mặt đất đến mắt bạn B cũng là 1,5 m. Biết chiều cao của tòa nhà là h = 20 m (Hình 17). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)?
Phương pháp giải - Xem chi tiết
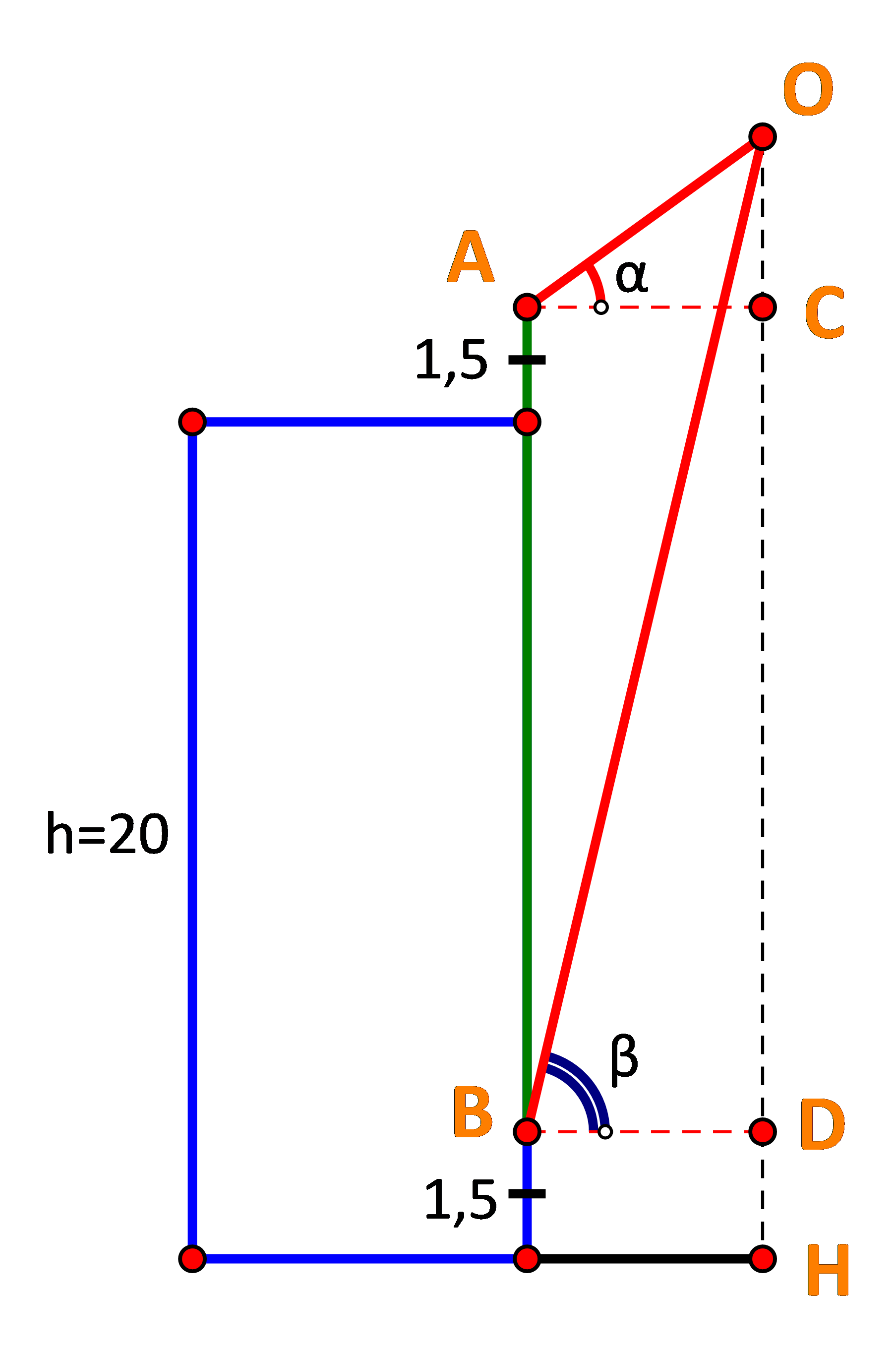
Bước 1: Vẽ hình, gọi các điểm O, C, D, H như hình vẽ.
Bước 2: Đặt x = OC. Tính AC, BD theo \(x,\alpha ,\beta \).
Bước 3: Lập luận tìm x. Từ đó suy ra khoảng cách OH.
Lời giải chi tiết
Gọi các điểm:
O là vị trí của chiếc diều.
H là hình chiếu vuông góc của chiếc diều trên mặt đất.
C, D lần lượt là hình chiếu vuông góc của A, B trên OH.
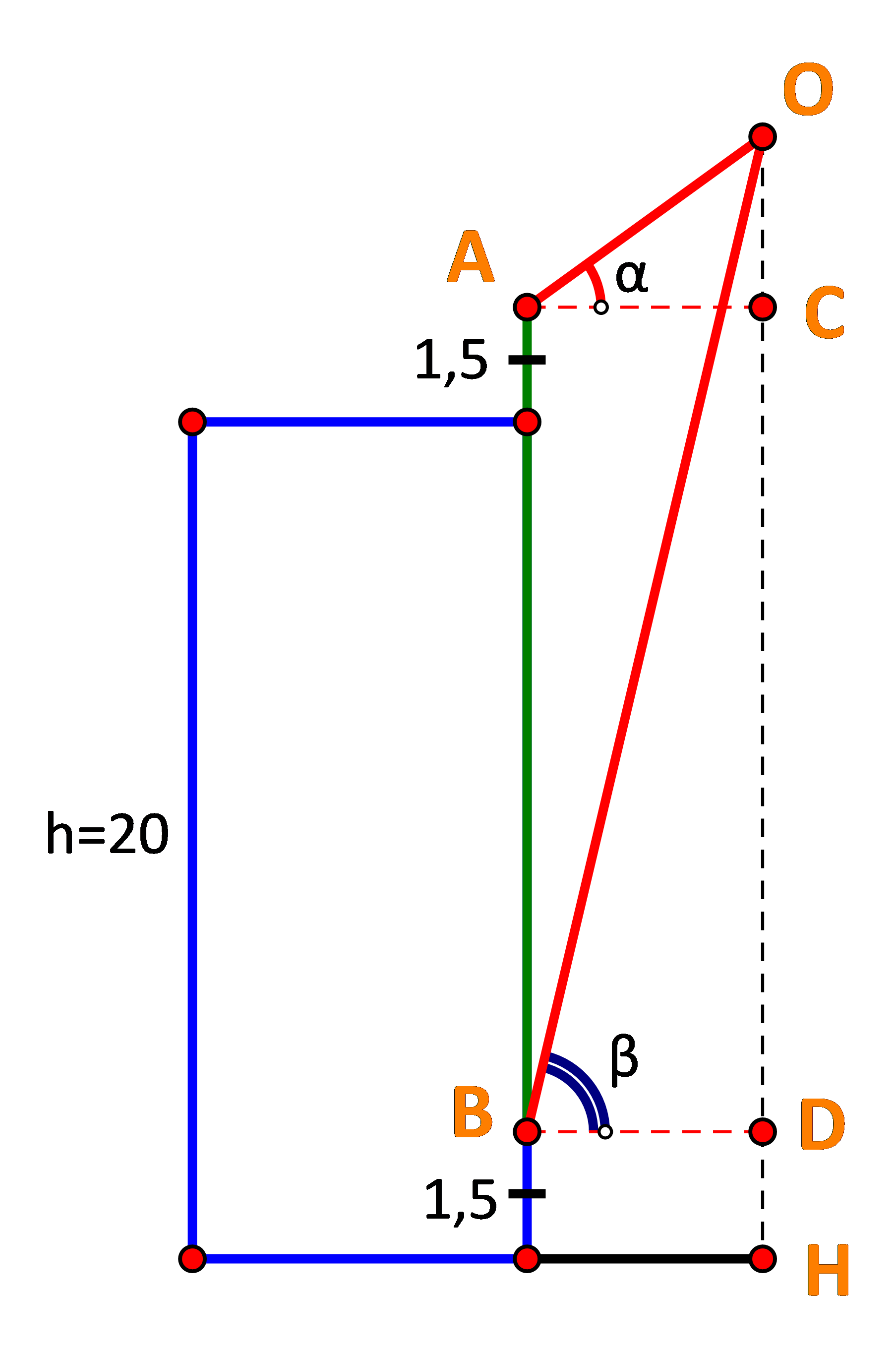
Đặt OC = x, suy ra OH = x + 20 + 1,5 =x + 21,5.
Xét tam giác OAC, ta có: \(\tan \alpha = \frac{{OC}}{{AC}} \Rightarrow AC = \frac{{OC}}{{\tan \alpha }} = \frac{x}{{\tan {{35}^o}}}\)
Xét tam giác OBD, ta có: \(\tan \beta = \frac{{OD}}{{BD}} \Rightarrow BD = \frac{{OD}}{{\tan \beta }} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
Mà:\(AC = BD\)\( \Rightarrow \frac{x}{{\tan {{35}^o}}} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
\(\begin{array}{l} \Leftrightarrow x.\tan {75^o} = \left( {x + 20} \right).\tan {35^o}\\ \Leftrightarrow x = \frac{{20.\tan {{35}^o}}}{{\tan {{75}^o} - \tan {{35}^o}}} \approx 4,6\end{array}\)
Suy ra OH = 26,1.
Vậy chiếc diều bay cao 26,1 m so với mặt đất.
