Đề bài
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB} \) và \(\overrightarrow {{F_3}} = \overrightarrow {OC} \) cùng tác động vào một vật tại điểm O và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} \)đều là 120 N và \(\widehat {AOB} = {120^o}\). Tìm cường độ và hướng của lực \(\overrightarrow {{F_3}} .\)
Phương pháp giải - Xem chi tiết
Bước 1: Xác định vecto tổng \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \)(hướng, độ lớn)
Bước 2: Từ giả thiết “vật đứng yên” suy ra cường độ và hướng của lực \(\overrightarrow {{F_3}} .\)
Lời giải chi tiết

Gọi D là đỉnh thứ tư của hình bình hành OADB.
Khi đó ta có: \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD} \)
Ta có: OA = OB = 120 suy ra tứ giác OADB là hình thoi
\( \Rightarrow \widehat {AOD} = \widehat {BOD} = \frac{{{{120}^o}}}{2} = {60^o}\)
\( \Rightarrow \Delta AOD\) đều (do OA = AD và \(\widehat {AOD} = {60^o}\))
\( \Rightarrow OD = OA = 120\)
Mặt khác: Do vật đứng yên nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \Leftrightarrow \;\overrightarrow {{F_3}} = - (\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} ) = - \overrightarrow {OD} \)
Suy ra vecto \(\overrightarrow {OC} \) là vecto đối của vecto \(\overrightarrow {OD} \)
Lại có: \(\widehat {COA} = {180^o} - \widehat {AOD} = {120^o}\).Tương tự: \(\widehat {COB} = {120^o}\)
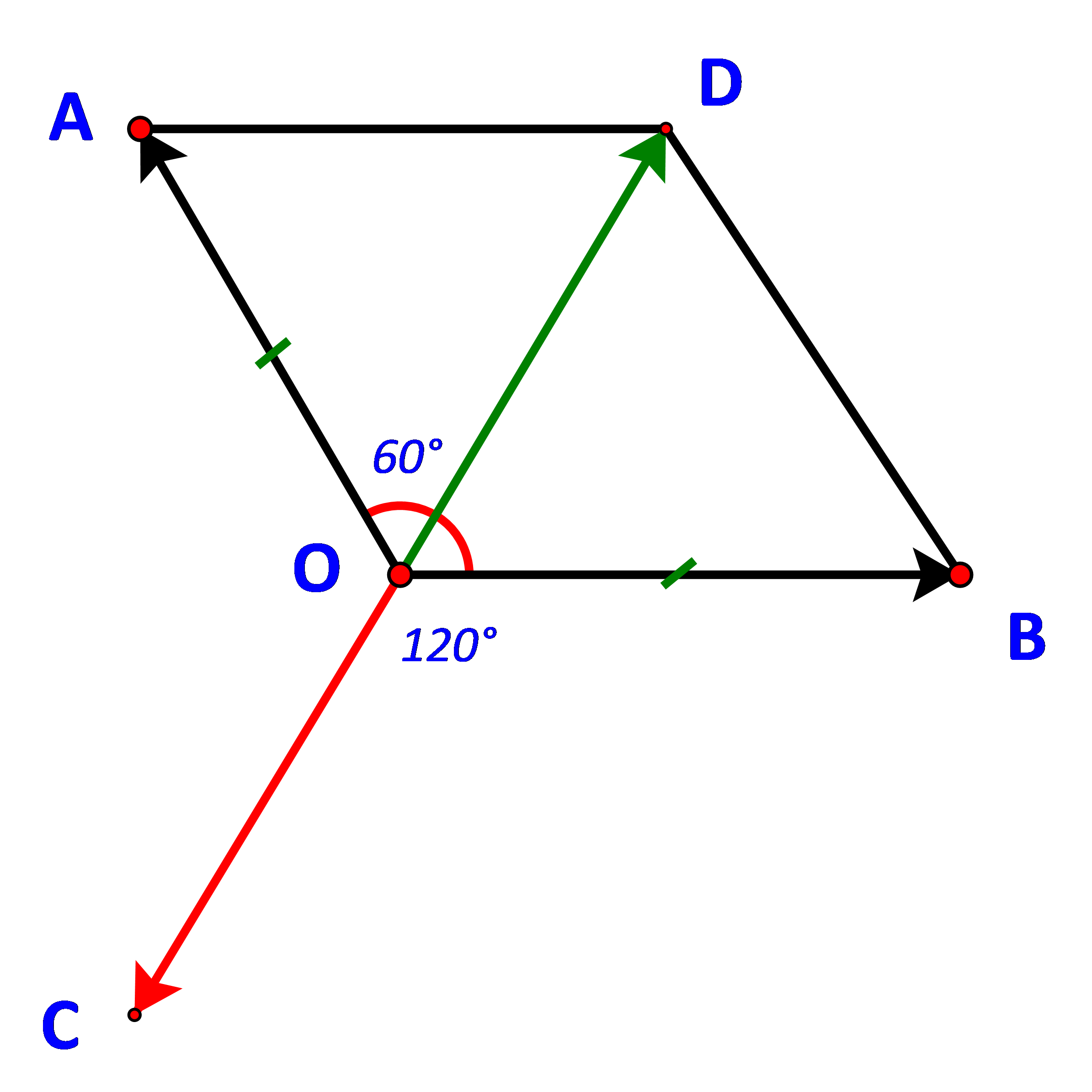
Vậy cường độ của lực \(\overrightarrow {{F_3}} \)là 120 N, tạo với lực\(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} \) góc \({120^o}\).
