Đề bài
Cho góc nhọn xOy và điểm M nằm trong góc xOy. Gọi E, F là hai điểm nằm ngoài góc xOy sao cho Ox là đường trung trực của đoạn thẳng ME, Oy là đường trung trực của đoạn thẳng MF (Hình 55).
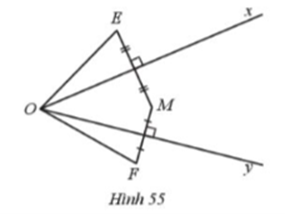
Chứng minh:
a) O là giao điểm ba đường trung trực của tam giácEMF.
b) Nếu \(\widehat {xOy} = 30^\circ \) thì \(\widehat {EOF} = 60^\circ \).
Phương pháp giải - Xem chi tiết
- Gọi O là giao điểm hai đường trung trực của ME và MF chứng minh O là giao điểm ba đường trung trực của tam giác EMF.
- Cho \(\widehat {xOy} = 30^\circ \) chứng minh: \(\widehat {EOM} = 2\widehat {xOM}\) và \(\widehat {MOF} = 2\widehat {MOy}\) từ đó chứng minh
\(\widehat {EOF} = \widehat {EOM} + \widehat {MOF} = 2\widehat {xOM} + 2\widehat {MOy}\)\( = 2\left( {\widehat {xOM} + \widehat {MOy}} \right) = 2\widehat {xOy} = 2.30^\circ = 60^\circ \)
Lời giải chi tiết
a) Trong tam giác EMF có O là giao điểm hai đường trung trực của ME và MF nên O là giao điểm ba đường trung trực của tam giác EMF.
Vậy O là giao điểm ba đường trung trực của tam giác FEM.
b)
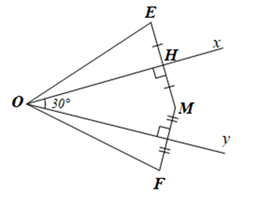
Gọi H là trung điểm của EM.
Xét ∆OEH và ∆OMH có:
\(\widehat {OHE} = \widehat {OHM}\left( { = 90^\circ } \right)\)
OH là cạnh chung,
EH = MH (do H là trung điểm của EM).
Do đó ∆OEH = ∆OMH (hai cạnh góc vuông).
Suy ra \(\widehat {{\rm{EOH}}} = \widehat {MOH}\) (hai góc tương ứng).
Do đó Ox là tia phân giác của góc EOM nên \(\widehat {{\rm{EOx}}} = \widehat {xOM} = \frac{1}{2}\widehat {{\rm{EOM}}}\)
Hay \(\widehat {EOM} = 2\widehat {xOM}\).
Chứng minh tương tự ta cũng có: \(\widehat {{\rm{FOy}}} = \widehat {MOy} = \frac{1}{2}\widehat {{\rm{MOF}}}\)
Hay\(\widehat {MOF} = 2\widehat {MOy}\)
Ta có: \(\widehat {EOF} = \widehat {EOM} + \widehat {MOF} = 2\widehat {xOM} + 2\widehat {MOy}\)\( = 2\left( {\widehat {xOM} + \widehat {MOy}} \right) = 2\widehat {xOy} = 2.30^\circ = 60^\circ \)
Vậy nếu \(\widehat {xOy} = 30^\circ \) thì \(\widehat {EOF} = 60^\circ \).
