Đề bài
Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.
Phương pháp giải - Xem chi tiết
-Chứng minh \(\Delta ABD = \Delta ACD\left( {c - g - c} \right)\)
Lời giải chi tiết
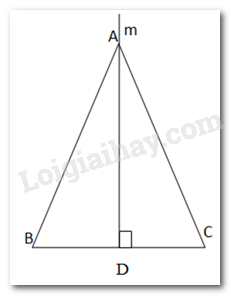
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC.
\( \Rightarrow \) AD là đường trung tuyến của BC.
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(\begin{array}{l}\widehat {ADB} = \widehat {ADC} = {90^0}\\AD:chung\\BD = CD\left( {gt} \right)\\ \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow AB = AC\)(2 cạnh tương ứng)
\( \Rightarrow \Delta ABC\)cân tại A (đpcm).
