Đề bài
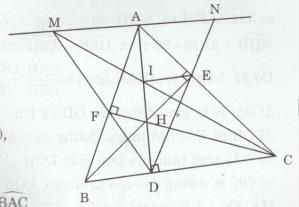
Cho tam giác nhọn ABC, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh rằng : \(\Delta BDA \sim \Delta BFC\) và BD.BC = BF.BA
b) Chứng minh rằng \(\widehat {BDF} = \widehat {BAC}\) .
c) CHứng minh rằng BH.BE = BD.BC và \(BH.BE{\rm{ }} + {\rm{ }}CH.CF{\rm{ }} = B{C^2}\) .
d) Đường thẳng qua A song song với BC cắt tia DF tại M. Gọi I là giao điểm của CM và AD. Chứng minh rằng IE // BC.
Lời giải chi tiết
a) Xét ∆BDA và ∆BFC có:
\(\widehat {DBA}\) (chung), \(\widehat {BDA} = \widehat {BFC}( = 90^\circ )\)
Do đó \(\Delta BDA \sim \Delta BFC(g.g)\)
\( \Rightarrow {{BD} \over {BF}} = {{BA} \over {BC}} \)
\(\Rightarrow BD.BC = BF.BA\)
b) Xét ∆BDF và ∆BAC có: \(\widehat {DBF}(chung),\)
\({{BD} \over {BA}} = {{BF} \over {BC}}\) (vì BD.BC = BF.BA)
Do đó \(\Delta BDF \sim \Delta BAC(c.g.c) \)
\(\Rightarrow \widehat {BDF} = \widehat {BAC}\)
c) Xét ∆BDH và ∆BEC có: \(\widehat {DBH}(chung),\widehat {BDH} = \widehat {BEC}( = 90^\circ )\)
Do đó \(\Delta BDH \sim \Delta BEC(g.g) \)
\(\Rightarrow {{BD} \over {BE}} = {{BH} \over {BC}} \)
\(\Rightarrow BH.BE = BD.BC\)
Tương tự có \(\Delta CDH \sim \Delta CFB \)
\(\Rightarrow {{CH} \over {BC}} = {{CD} \over {CF}}\)
\(\Rightarrow CH.CF = CD.BC\)
Do đó \(BH.BE + CH.CF \)\(\,= BD.BC + CD.BC\)\(\, = BC.(BD + CD) = BC.BC= {BC^2}\)
d) Gọi N là giao điểm của DE và AM, ta có \(\widehat {BDF} = \widehat {BAC}(\Delta BDF \sim \Delta BAC)\)
Tương tự \(\widehat {CDE} = \widehat {CAB}\)
Do đó \(\widehat {BDF} = \widehat {CDE}.\)
Mà \(\widehat {BDF} + \widehat {ADM} = \widehat {CDE} + \widehat {ADN}( = 90^\circ ) \)
\(\Rightarrow \widehat {ADM} = \widehat {ADN}\)
Mặt MN // BC, \(AD \bot BC \Rightarrow MN \bot AD\)
∆DMN có DA là đường cao, đường phân giác
\( \Rightarrow \Delta DMN\) cân tại D => AM = AN
Xét ∆IDC có: AM // CD \( \Rightarrow {{AM} \over {CD}} = {{AI} \over {DI}}\) (hệ quả của định lí Thales)
Xét ∆EDC có: CD // AN \( \Rightarrow {{AN} \over {CD}} = {{AE} \over {CE}}\) (hệ quả của định lí Thales) \( \Rightarrow {{AI} \over {DI}} = {{AE} \over {CE}}\)
Xét ∆AND có: \({{AI} \over {DI}} = {{AE} \over {CE}} \Rightarrow IE//AN\) (định lí Thales đảo)
Ta có IE // AN và AN // BC => IE // BC
soanvan.me
