Đề bài
Hình khối sau đây có phải là hình lăng trụ đứng không ? Tính thể tích và diện tích toàn phần của khối.
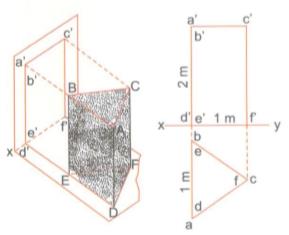
Lời giải chi tiết
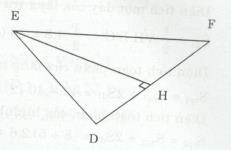
Theo đề bài ta có \(BC = AC = 1m,BE = AD = 2m,\)
\(EF = DF = 1m,AB = ED = 1m\)
Do đó: ∆ABC = ∆DEF và các tứ giác BEFC, BEDA, ACFD đều là hình chữ nhật
Vậy nên khối đã cho là lăng trụ đứng có đáy là tam giác đều, cạnh 1m
Chiều cao EH của tam giác đáy là:
\(EH = \sqrt {E{D^2} - D{H^2}} = \sqrt {1 - 0,{5^2}}\)\(\, = {{\sqrt 3 } \over 2}(m)\)
Thế tích của lăng trụ là:
\(V = {S_d}.h = {1 \over 2}.EH.DF.AD \)\(\,= {1 \over 2}.{{\sqrt 3 } \over 2}.1.2 = {{\sqrt 3 } \over 2}({m^3})\)
Diện tích xung quanh của lăng trụ là:
\({S_{xq}} = 2p.h = 3DE.AD = 3.1.2 \)\(\,= 6({m^2})\)
Diện tích toàn phần của lăng trụ là:
\({S_{tp}} = {S_{xq}} + 2{S_d} = 6 + 2.{{\sqrt 3 } \over 4} \)\(\,= {{12 + \sqrt 3 } \over 2}({m^2})\)
soanvan.me
