Đề bài
Tính diện tích toàn phần của hình chóp tứ giác đều có cạnh bên dài 20 cm và cạnh đáy dài 10 cm.
Lời giải chi tiết
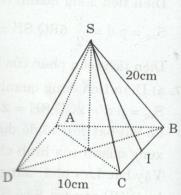
Kẻ \(SI \bot BC\) tại I
∆SBC cân tại S => SI là đường trung tuyến
=> I là trung điểm của BC \( \Rightarrow BI = {{BC} \over 2} = 5(cm)\)
∆SBI vuông tại I có \(S{I^2} + I{B^2} = S{B^2}\) (định lí Py-ta-go)
\( \Rightarrow S{I^2} + {5^2} = {20^2} \Rightarrow S{I^2} = 375\)
\(\Rightarrow SI = \sqrt {375} (cm)\)
Diện tích đáy của hình chóp:
\({S_d} = C{D^2} = {10^2} = 100(c{m^2})\) (vì ABCD là hình vuông)
Diện tích xung quanh của hình chóp:
\({S_{xq}} = p.d = 2.CD.SI \)\(\,= 2.10.\sqrt {375} = 20\sqrt {375} (c{m^2})\)
Diện tích toàn phần của hình chóp: \({S_{tp}} = {S_{xq}} + {S_d} = 20\sqrt {375} + 100(c{m^2})\)
soanvan.me
