Đề bài
Cho hai đường thẳng a và b cắt nhau tại điểm O và đường thẳng c cắt mp(a , b) ở điểm I khác O. Gọi M là điểm di động trên c và khác I. Chứng minh rằng giao tuyến của các mặt phẳng (M , a), (M , b) nằm trên một mặt phẳng cố định.
Lời giải chi tiết
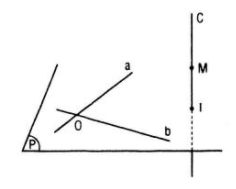
Ta có:
\(\left\{ \begin{array}{l}
M \in \left( {M,a} \right)\\
M \in \left( {M,b} \right)
\end{array} \right. \)
\(\Rightarrow M \in \left( {M,a} \right) \cap \left( {M,b} \right)\)
Vì \(O = a \cap b\)
\( \Rightarrow \left\{ \begin{array}{l}
O \in a \subset \left( {M,a} \right)\\
O \in b \subset \left( {M,b} \right)
\end{array} \right.\)
nên \(O \in \left( {M,a} \right) \cap \left( {M,b} \right) \)
\(\Rightarrow \left( {M,a} \right) \cap \left( {M,b} \right) = MO\)
Vì M \(\in\) c nên MO ⊂ mp(O, c)
Vậy giao tuyến của hai mặt phẳng (M, a), (M, b) nằm trên mặt phẳng (O, c) cố định.
soanvan.me
