Đề bài
Cho tứ diện ABCD. Các điểm P, Q lần lượt là trung điểm của AB và CD; điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp(PQR) và cạnh AD. Chứng minh rằng AS = 2SD.
Phương pháp giải - Xem chi tiết
Áp dụng định lí Menelaus để giải bài toán
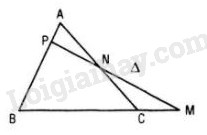
Giả sử đường thẳng Δ cắt các cạnh (hoặc phần kéo dài) BC, CA, AB lần lượt tại M, N, P thì :
\({{MB} \over {MC}}.{{NC} \over {NA}}.{{PA} \over {PB}} = 1\)
Lời giải chi tiết
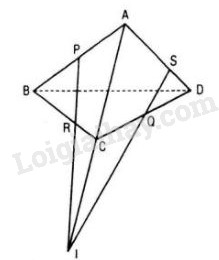
Trong (ABC), gọi {I} = PR ∩ AC
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
\left( {PQR} \right) \cap \left( {ABC} \right) = PR\\
\left( {ABC} \right) \cap \left( {ACD} \right) = AC\\
\left( {PQR} \right) \cap \left( {ACD} \right) = Qt\\
AC \cap PR = I
\end{array} \right.\\
\Rightarrow I \in Qt
\end{array}\)
Trong mp(ACD) gọi {S} = QI ∩ AD
Thì {S} = AD ∩ (PQR)
Áp dụng định lí Menelaus trong tam giác ABC với cát tuyến PRI ta có
\({{PA} \over {PB}}.{{RB} \over {RC}}.{{IC} \over {IA}} = 1 \)\(\Rightarrow 1.2.{{IC} \over {IA}} = 1\)
\( \Rightarrow {{IC} \over {IA}} = {1 \over 2}\) ⇒ C là trung điểm của AI.
Áp dụng định lí Menelaus trong tam giác ACD với cát tuyến IQS ta có :
\({{IC} \over {IA}}.{{SA} \over {SD}}.{{QD} \over {QC}} = 1 \Rightarrow {1 \over 2}.{{SA} \over {SD}}.1 = 1 \)
\(\Rightarrow SA = 2SD\,\,\left( {dpcm} \right)\)
soanvan.me
