Video hướng dẫn giải
Giải các phương trình:
LG a
a) \(\sin (x + 1) = {2 \over 3}\)
Phương pháp giải:
Giải phương trình lượng giác cơ bản của hàm sin.
Lời giải chi tiết:
Ta có:
\(\eqalign{
& \sin (x + 1) = {2 \over 3} \cr
& \Leftrightarrow \left[ \matrix{
x + 1 = \arcsin {2 \over 3} + k2\pi \hfill \cr
x + 1 = \pi - \arcsin {2 \over 3} + k2\pi \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
x = - 1 + \arcsin {2 \over 3} + k2\pi \hfill \cr
x = - 1 + \pi - \arcsin {2 \over 3} + k2\pi \hfill \cr} \right.;k \in \mathbb{Z} \cr} \)
Vậy nghiệm của phương trình là \(x = - 1 + \arcsin \frac{2}{3} + k2\pi ;\) \(x = - 1 + \pi - \arcsin \frac{2}{3} + k2\pi \,\,\left( {k \in Z} \right)\)
LG b
\({\sin ^2}2x = {1 \over 2}\)
Phương pháp giải:
Sử dụng công thức hạ bậc.
Lời giải chi tiết:
Ta có:
\(\eqalign{
& {\sin ^2}2x = {1 \over 2} \Leftrightarrow {{1 - \cos 4x} \over 2} = {1 \over 2} \cr
& \Leftrightarrow \cos 4x = 0 \Leftrightarrow 4x = {\pi \over 2} + k\pi \cr
& \Leftrightarrow x = {\pi \over 8} + k{\pi \over 4},k \in \mathbb{Z} \cr} \)
Vậy nghiệm của phương trình là \(x = \frac{\pi }{8} + \frac{{k\pi }}{4}\,\,\left( {k \in Z} \right)\).
Cách khác:
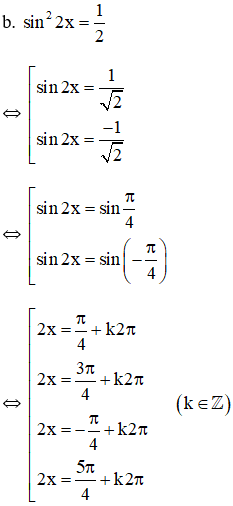
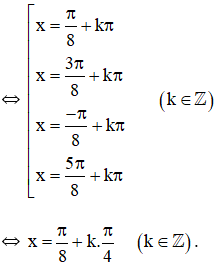
Có thể để nguyên các họ nghiệm không nhất thiết phải gộp nghiệm.
LG c
\({\cot ^2}{x \over 2} = {1 \over 3}\)
Phương pháp giải:
Lấy căn bậc hai hai vế. Giải phương trình lượng giác cơ bản của hàm cot.
Lời giải chi tiết:
\(DK:\frac{x}{2} \ne k\pi \Leftrightarrow x \ne k2\pi \)
Ta có:
\(\eqalign{
& {\cot ^2}{x \over 2} = {1 \over 3} \Leftrightarrow \left[ \matrix{
\cot {x \over 2} = {{\sqrt 3 } \over 3} \,\,\,\,\,\,\,\,\,(1) \hfill \cr
\cot {x \over 2} = - {{\sqrt 3 } \over 3}\,\,\,\,(2) \hfill \cr} \right. \cr
& (1) \Leftrightarrow \cot {x \over 2} = \cot {\pi \over 3} \cr &\Leftrightarrow {x \over 2} = {\pi \over 3} + k\pi \cr
& \Leftrightarrow x = {{2\pi } \over 3} + k2\pi ,k \in \mathbb{Z} \cr
& (2) \Leftrightarrow \cot {x \over 2} = \cot ( - {\pi \over 3}) \cr&\Leftrightarrow {x \over 2} = - {\pi \over 3} + k\pi \cr
& \Leftrightarrow x = - {{2\pi } \over 3} + k2\pi ;k \in \mathbb{Z} (TM)\cr} \)
Vậy nghiệm của phương trình là \(x = \pm \frac{{2\pi }}{3} + k2\pi \,\,\left( {k \in Z} \right)\).
Chú ý:
\(\cot \left( { - \frac{{\sqrt 3 }}{3}} \right) = \cot \left( {\frac{{2\pi }}{3}} \right)\) nên khi giải pt (2) cũng có thể đưa về góc \({\frac{{2\pi }}{3}}\).
LG d
\(\tan ({\pi \over {12}} + 12x) = - \sqrt 3 \)
Phương pháp giải:
Giải phương trình lượng giác cơ bản của hàm tan.
Lời giải chi tiết:
\(DK:\frac{\pi }{{12}} + 12x \ne \frac{\pi }{2} + k\pi \) \(\Leftrightarrow 12x \ne \frac{{5\pi }}{{12}} + k\pi \) \( \Leftrightarrow x \ne \frac{{5\pi }}{{144}} + \frac{{k\pi }}{{12}}\)
Ta có:
\( \tan ({\pi \over {12}} + 12x) = - \sqrt 3\)
\(\Leftrightarrow \tan ({\pi \over {12}} + 12x ) = \tan ({{ - \pi } \over 3})\)
\(\Leftrightarrow {\pi \over {12}} + 12x = {{ - \pi } \over 3} + k\pi\)
\(\Leftrightarrow x = - {{5\pi } \over {144}} + k{\pi \over {12}},k \in \mathbb{Z} (TM) \)
Vậy nghiệm của phương trình đã cho là: \(x = {{ - 5\pi } \over {144}} + {{k\pi } \over {12}},k \in \mathbb{Z}\)
soanvan.me
