Lựa chọn câu để xem lời giải nhanh hơn

5.4.

Cho hai điện trở, R1=15Ω chịu được dòng điện có cường độ tối đa 2A và R2=10Ω chịu được dòng điện có cường độ tối đa 1A. Hiệu điện thế tối đa có thể đặt vào hai đầu đoạn mạch gồm R1 và R2 mắc song song là:

A. 40V         B. 10V       C. 30V         D. 25V

Phương pháp giải:

Vận dụng biểu thức tính chất của đoạn mạch mắc song song

Lời giải chi tiết:

Ta có:

\({U_1} = {\text{ }}{I_1}.{R_1} = {\text{ }}{2_.}15{\text{ }} = {\text{ }}30V\); \({\text{ }}{U_2} = {\text{ }}{I_2}.{R_2} = {\text{ }}1.10{\text{ }} = {\text{ }}10V\)

Vì R1 // R2 nên \(U = U_1 = U_2= 10V\).

=> Chọn B

5.5.

Cho mạch điện có sơ đồ như hình 5.4, vôn kế chỉ 36V, ampe kế chỉ 3A, R1=30Ω.
 
 
a. Tính điện trở R2.
b. Tính số chỉ của các ampe kế A1 và A2.

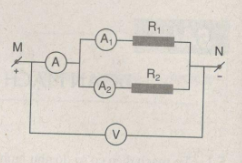
Phương pháp giải:

+ Sử dụng biểu thức tính điện trở tương đương của đoạn mạch mắc song song: \(\dfrac{1}{R}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\)
+ Sử dụng biểu thức định luật Ôm: \(I=\dfrac{U}{R}\)

Lời giải chi tiết:

a) Điện trở R2 là:
Ta có: \(\dfrac{R_1R_2}{R_1+R_2}=\dfrac{U}{I}=\dfrac{36}{3}=12\Omega\)

Thay \(R_1=30Ω\) ta được:

\(\eqalign{
& {{30.{R_2}} \over {30 + {R_2}}} = 12\cr& \Rightarrow 30{R_2} = 12.\left( {30 + {R_2}} \right) \cr 
& \Rightarrow 30{R_2} = 360 + 12{R_2} \cr 
& \Rightarrow 30{R_2} - 12{R_2} = 360 \cr 
& \Rightarrow 18{R_2} = 360 \cr 
& \Rightarrow {R_2} = {{360} \over {18}} = 20\,\Omega \cr} \)

b) Số chỉ của ampe kế A1 là: \({I_1} = \dfrac{U}{ {{R_1}}} = \dfrac{{36} }{{30}} = 1,2A\)
   Số chỉ của ampe kế A2 là: \({I_2} = I - {I_1} = 3 - 1,2 = 1,8A\)

5.6.

a) Điện trở tương đương của đoạn mạch là: 
b) Cường độ dòng điện chạy qua mạch chính và từng mạch rẽ là:

Lời giải chi tiết:

a) Điện trở tương đương của đoạn mạch là: 

\(\begin{array}{l}{R_{23}} = \dfrac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} = \dfrac{{20.20}}{{20 + 20}} = 10\Omega \\{R_{td}} = \dfrac{{{R_1}{R_{23}}}}{{{R_1} + {R_{23}}}} = \dfrac{{10.10}}{{10 + 10}} = 5\Omega \end{array}\)

b) Cường độ dòng điện chạy qua mạch chính và từng mạch rẽ là:
\(\begin{array}{l}{I_1} = \dfrac{U}{{{R_1}}} = \dfrac{{12}}{{10}} = 1,2A\\{I_2} = {I_3} = \dfrac{{12}}{{20}} = 0,6A\\I = {I_1} + {I_2} + {I_3} = 1,2 + 0,6 + 0,6 = 2,4A\end{array}\)
soanvan.me