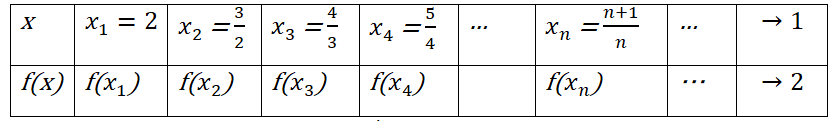Video hướng dẫn giải
Xét hàm số:
\(\displaystyle f(x) = {{2{x^2} - 2x} \over {x - 1}}\)
LG 1
Cho biến \(x\) những giá trị khác 1 lập thành dãy số \({x_n},{\rm{ }}{x_n}\; \to {\rm{ }}1\) như trong bảng sau:
Khi đó, các giá trị tương ứng của hàm số
\(f({x_1}),{\rm{ }}f({x_2}), \ldots ,{\rm{ }}f({x_n}),{\rm{ }} \ldots \)
cũng lập thành một dãy số mà ta kí hiệu là \((f({x_n})).\)
a) Chứng minh rằng \(f\left( {{x_n}} \right) = 2{x_n} = \dfrac{{2n + 2}}{n}\)
b) Tìm giới hạn của dãy số \((f({x_n})).\)
Phương pháp giải:
a) Tính và rút gọn \(f\left( {{x_n}} \right)\) suy ra đáp số, chú ý \(x_n=\dfrac{{n + 1}}{n}\).
b) Xét giới hạn \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2)\) và suy ra đáp số.
Lời giải chi tiết:
a) \(\displaystyle f({x_n}) = {{2{x_n}^2 - 2{x_n}} \over {{x_n} - 1}} = {{2{x_n}({x_n} - 1)} \over {{x_n} - 1}} \) \(= 2{x_n}\)
\(\displaystyle {x_n} = {{n+1} \over {n}} \) \(\displaystyle \Rightarrow f({x_n}) = 2{x_n} = 2.{{n+1} \over {n}} = {{2n+2} \over {n}}\)
b) \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2) \) \(\displaystyle = \mathop {\lim }\limits_{n \to + \infty } ({{2n+2} \over {n}} - 2) = \mathop {\lim }\limits_{n \to + \infty } {{ 2} \over {n}}\)
Ta có: \(\displaystyle \mathop {\lim }\limits_{n \to + \infty } {{ 2} \over {n}} = 0 \) \(\displaystyle \Rightarrow \mathop {\lim }\limits_{n \to + \infty } (f({x_n}) - 2) = 0 \) \(\displaystyle \Rightarrow \mathop {\lim }\limits_{n \to + \infty } f({x_n}) = 2\)
LG 2
Chứng minh rằng với dãy số bất kì \({x_n},{\rm{ }}{x_n}\; \ne {\rm{ }}1\) và \({x_n}\; \to {\rm{ }}1\), ta luôn có \(\;f({x_n}) \to 2.\)
(Với tính chất thể hiện trong câu 2, ta nói hàm số \(\displaystyle f(x) = {{2{x^2} - 2x} \over {x - 1}}\) có giới hạn là 2 khi \(x\) dần tới 1).
Phương pháp giải:
Tính \(\lim f({x_n})\) dựa vào công thức có được ở phần 1a.
Lời giải chi tiết:
\(\lim f({x_n}) = \lim\,2{x_n} \) \(= 2\lim {x_n} = 2.1 = 2\)
soanvan.me