Đề bài
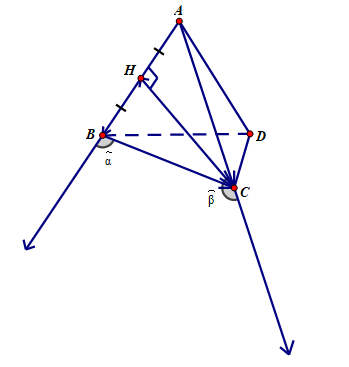
Cho tứ diện đều \(ABCD\) có \(H\) là trung điểm của cạnh \(AB\). Hãy tính góc giữa các cặp vecto sau đây:
a) \(\overrightarrow {AB}\) và \(\overrightarrow {BC}\)
b) \(\overrightarrow {CH}\) và \(\overrightarrow {AC}\)
Video hướng dẫn giải
Lời giải chi tiết
Tứ diện \(ABCD\) đều có các mặt là tam giác đều.
a) Góc giữa \(\overrightarrow {AB}\) và \(\overrightarrow {BC}\) là góc \(\alpha \) và \(\alpha = {180^0} - {60^0} = {120^0}\)
b) Góc giữa \(\overrightarrow {CH}\) và \(\overrightarrow {AC}\) là góc \(\beta \)
\(H\) là trung điểm cạnh \(AB\) của tam giác đều \(ABC\) nên \(CH\) vừa là trung tuyến vừa là đường cao nên \(CH ⊥ AB\)
Xét tam giác vuông \(ACH\) tại \(H\) có \(\widehat {ACH} + \widehat {CAH} = {90^0} \) \(\Rightarrow \widehat {ACH} = {90^0} - {60^0} = {30^0}\)
Nên \(\beta = {180^0} - {30^0} = {150^0}\)
soanvan.me