HĐ 1
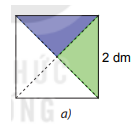
Cắt một hình vuông cạnh bằng 2 dm, rồi cắt nó thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông (H.2.2.a)
Phương pháp giải:
Cắt theo mô tả của đề bài
Lời giải chi tiết:
Bước 1: Cắt một hình vuông cạnh bằng 2 dm
Bước 2: Cắt hình vuông thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông.
HĐ 2
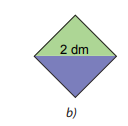
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2.b). Em hãy tính diện tích hình vuông nhận được.
Phương pháp giải:
Ghép 2 tam giác như hình.
Diện tích hình vuông = Diện tích hình vuông ban đầu (cạnh 2 dm) : 2
Lời giải chi tiết:
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông.
Vì 2 tam giác vuông chiếm một nửa hình vuông ban đầu nên
Diện tích hình vuông thu được là:
2.2:2= 2 (dm2)
HĐ 3
Dùng thước có vạch chia để đo độ dài cạnh hình vuông nhận được trong HĐ2. Độ dài cạnh hình vuông này bằng bao nhiêu đềximét ?
Phương pháp giải:
Bước 1: Dùng thước đo cạnh hình vuông nhận được trong HĐ2, ta được số liệu có đơn vị cm.
Bước 2: Đổi đơn vị cm sang dm.
Lời giải chi tiết:
Dùng thước đo ta được cạnh hình vuông dài khoảng 14 cm.
Ta có: 14 cm = 1,4 dm
Vận dụng
Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, tức là lấy chu vi thân cây chia làm 8 phần bằng nhau (quân bát); bớt đi ba phần (phát tam) còn lại 5 phần (tổn ngũ) rồi chia đôi kết quả (quân nhị). Hãy cho biết người xưa đã ước lượng số \(\pi \) bằng bao nhiêu?
Phương pháp giải:
Từ công thức tính chu vi đường tròn: C = \(\pi \). d \(a = \sqrt S \)\( \Rightarrow d = \frac{C}{\pi }\)\(\)
Thực hiện theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”
Lời giải chi tiết:
Theo quy tắc “quân bát, phát tam, tổn ngũ, quân nhị”, có: \(d = \frac{C}{8}.5:2 = \frac{C}{8}.5.\frac{1}{2} = \frac{{5C}}{{16}} = \frac{C}{{\frac{{16}}{5}}}\)
Theo công thức, có: \(d = \frac{C}{\pi }\)
Như vậy, người xưa đã ước lượng số \(\pi \) bằng \(\frac{{16}}{5} = 3,2\).