Luyện tập 1
a) Trong các cách viết: \(\sqrt 2 \in \mathbb{Q}; \pi \in \mathbb{I}; 15 \in \mathbb{R}\), cách viết nào đúng?
b) Viết số đối của các số: \(5,08(299); - \sqrt 5 \)
Phương pháp giải:
Số hữu tỉ là số viết được dưới dạng \(\frac{a}{b}(a,b \in \mathbb{Z};b \ne 0)\)
Số hữu tỉ và số vô tỉ được gọi chung là số thực
Số đối của số thực a là -a
Lời giải chi tiết:
a) Ta có: \(\sqrt 2 \notin \mathbb{Q};\pi \in \mathbb{I};15 \in \mathbb{R}\)
Vậy cách viết \(\pi \in \mathbb{I}; 15 \in \mathbb{Q}\) là đúng
b) Số đối của 5,08(299) là -5,08(299)
Số đối của -\(\sqrt 5 \) là \(\sqrt 5 \)
Câu hỏi
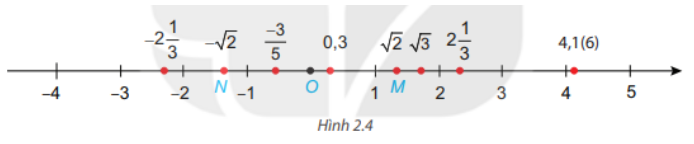
Điểm nào trong Hình 2.4 biểu diễn số \( - \sqrt 2 \)? Em có nhận xét gì về điểm biểu diễn của hai số đối nhau?
Phương pháp giải:
Quan sát trục số, tìm điểm \( - \sqrt 2 \)
Nhận xét điểm biểu diễn của hai số đối nhau
Lời giải chi tiết:
Điểm biểu diễn số \( - \sqrt 2 \) là điểm N.
Điểm biểu diễn của hai số đối nhau là 2 điểm cách đều gốc O và nằm về 2 phía của điểm O
Luyện tập 2
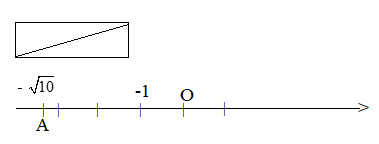
Cho biết nếu một tam giác vuông có hai cạnh góc vuông bằng 1 và 3 thì cạnh huyền của tam giác bằng \(\sqrt {10} \). Em hãy vẽ điểm biểu diễn số - \(\sqrt {10} \) trên trục số.
Phương pháp giải:
Bước 1: Vẽ tam giác vuông có hai cạnh góc vuông bằng 1 và 3. Đo độ dài của cạnh huyền
Bước 2: Vẽ trục số. Biểu diễn số - \(\sqrt {10} \) trên trục số nằm ở bên trái gốc O, cách O một khoảng bằng độ dài cạnh huyền của tam giác vuông vừa vẽ.
Lời giải chi tiết:
Chú ý: Các số thực âm được biểu diễn bởi các điểm nằm bên trái điểm O trên trục số.