HĐ Khám phá 1
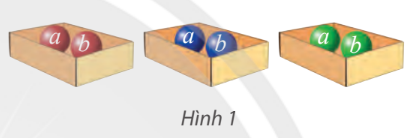
Có ba hộp, mỗi hộp đựng hai quả cầu được dán nhãn a và b (xem Hình 1). Lấy từ mỗi hộp một quả cầu. Có bao nhiêu cách lấy để trong ba quả cầu lấy ra:
a) có 3 quả cầu dán nhãn b?
b) có 2 quả cầu dán nhãn b?
c) có 1 quả cầu dán nhãn b?
d) không có quả cầu nào dán nhãn b?
Lời giải chi tiết:
a) Chỉ có 1 cách lấy 3 quả cầu đều là b (bằng \(C_3^3 = 1\))
b) Số cách lấy 2 quả cầu b từ 3 hộp (và 1 quả cầu a từ hộp còn lại) là \(C_3^2 = 3\)
c) Số cách lấy 1 quả cầu b từ 3 hộp (và 2 quả cầu a từ hộp còn lại) là \(C_3^1 = 3\)
d) Chỉ có 1 cách lấy 3 quả cầu mà khoongg có quả cầu b nào (bằng \(C_3^0 = 1\))
Thực hành 1
Hãy khai triển:
a) \({\left( {x - y} \right)^6}\)
b) \({\left( {1 + x} \right)^7}\)
Phương pháp giải:
a) \({(a + b)^6} = C_6^0{a^6} + C_6^1{a^5}b + C_6^2{a^4}{b^2} + C_6^3{a^3}{b^3} + C_6^4{a^2}{b^4} + C_6^5a{b^5} + C_6^6{b^6}\)
b) \({(a + b)^7} = C_7^0{a^7} + C_7^1{a^6}b + C_7^2{a^5}{b^2} + C_7^3{a^4}{b^3} + C_7^4{a^3}{b^4} + C_7^5{a^2}{b^5} + C_7^6a{b^6} + C_7^7{b^7}\)
Lời giải chi tiết:
a) Áp dụng công thức nhị thức Newton, ta có:
\(\begin{array}{l}{(x + ( - y))^6} = C_6^0{x^6} + C_6^1{x^5}( - y) + C_6^2{x^4}{( - y)^2} + C_6^3{x^3}{( - y)^3} + C_6^4{x^2}{( - y)^4} + C_6^5x{( - y)^5} + C_6^6{( - y)^6}\\ = {x^6} + 6{x^5}( - y) + 15{x^4}{( - y)^2} + 20{x^3}{( - y)^3} + 15{x^2}{( - y)^4} + 6x{( - y)^5} + {( - y)^6}\\ = {x^6} - 6{x^5}y + 15{x^4}{y^2} - 20{x^3}{y^3} + 15{x^2}{y^4} - 6x{y^5} + {y^6}\end{array}\)
b) Áp dụng công thức nhị thức Newton, ta có:
\(\begin{array}{l}{(1 + x)^7} = C_7^0{1^7} + C_7^1{1^6}x + C_7^2{1^5}{x^2} + C_7^3{1^4}{x^3} + C_7^4{1^3}{x^4} + C_7^5{1^2}{x^5} + C_7^61.{x^6} + C_7^7{x^7}\\ = 1 + 7x + 21{x^2} + 35{x^3} + 35{x^4} + 21{x^5} + 7{x^6} + {x^7}\end{array}\)
