Câu hỏi mục 2 trang 61, 62, 63, 64

HĐ2

Cho đường conic có tiêu điểm F, đường chuẩn \(\Delta \) và một điểm M là điểm nằm trên đường conic đó. Tìm mối liên hệ giữa tỉ số \(\frac{{MF}}{{d(M,\Delta )}}\) và tên gọi của đường conic đó.

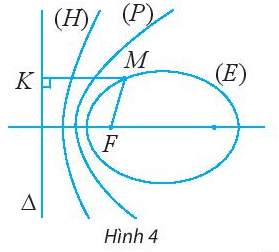
Lời giải chi tiết:

+ Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \(M(x;y) \in (E)\)

\(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{a + ex}}{{\frac{{a + ex}}{e}}} = e\), \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{{a - ex}}{{\frac{{a - ex}}{e}}} = e\)

Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = e = \frac{c}{a} < 1\)

+ Hypebol (H):  \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), \(M(x;y) \in (H)\)

\(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{\left| {a + ex} \right|}}{{\left| {x + \frac{a}{e}} \right|}} = \frac{{\left| {a + ex} \right|}}{{\frac{{\left| {a + ex} \right|}}{e}}} = e\); \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{\left| {a - ex} \right|}}{{\left| {x - \frac{a}{e}} \right|}} = \frac{{\left| {a - ex} \right|}}{{\frac{{\left| {a - ex} \right|}}{e}}} = e\) ;

Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = e = \frac{c}{a} > 1\)

+ Parabol (P)  \({y^2} = 2px\)

\(\frac{{MF}}{{d(M,\Delta )}} = e = 1\)

Kết luận các đường conic đều có \(\frac{{MF}}{{d(M,\Delta )}} = e\) và

\(\frac{{MF}}{{d(M,\Delta )}} < 1\) thì conic là đường elip

\(\frac{{MF}}{{d(M,\Delta )}} = 1\) thì conic là đường parabol

\(\frac{{MF}}{{d(M,\Delta )}} > 1\) thì conic là đường hypebol

Thực hành 2

Xác định tâm sai, tọa độ tiêu điểm và phương trình đường chuẩn tương ứng của mỗi đường conic sau:

a) \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{2} = 1\)

b) \(\frac{{{x^2}}}{{12}} - \frac{{{y^2}}}{4} = 1\)

c) \({y^2} = \frac{1}{2}x\)

Phương pháp giải:

a) Elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), \(c = \sqrt {{a^2} - {b^2}} \)

+ Tâm sai của elip: \(e = \frac{c}{a}\)

+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)

+ Đường chuẩn: \({\Delta _1}:x =  - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\).

b) Hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), \(c = \sqrt {{a^2} + {b^2}} \)

+ Tâm sai của hypebol: \(e = \frac{c}{a}\)

+ Tiêu điểm \({F_1}( - c;0),{F_2}(c;0)\)

+ Đường chuẩn: \({\Delta _1}:x =  - \frac{a}{e}\) và \({\Delta _2}:x = \frac{a}{e}\).

c) Parabol (P)  \({y^2} = 2px\)

+ Tâm sai \(e = 1\)

+ Tiêu điểm \(F(\frac{p}{2};0)\)

+ Đường chuẩn: \(\Delta :x =  - \frac{p}{2}\)

Lời giải chi tiết:

a) Elip (E): \(\frac{{{x^2}}}{5} + \frac{{{y^2}}}{2} = 1\), suy ra \(c = \sqrt {{a^2} - {b^2}}  = \sqrt 3 \)

+ Tâm sai của elip: \(e = \frac{c}{a} = \frac{{\sqrt 3 }}{{\sqrt 5 }} = \frac{{\sqrt {15} }}{5}\)

+ Tiêu điểm \({F_1}( - \sqrt 3 ;0),{F_2}(\sqrt 3 ;0)\)

+ Đường chuẩn: \({\Delta _1}:x =  - \frac{{5\sqrt 3 }}{3}\) và \({\Delta _2}:x = \frac{{5\sqrt 3 }}{3}\).

b) Hypebol (H): \(\frac{{{x^2}}}{{12}} - \frac{{{y^2}}}{4} = 1\), \(c = \sqrt {{a^2} + {b^2}}  = 4\)

+ Tâm sai của hypebol: \(e = \frac{c}{a} = \frac{4}{{2\sqrt 3 }} = \frac{{2\sqrt 3 }}{3}\)

+ Tiêu điểm \({F_1}( - 4;0),{F_2}(4;0)\)

+ Đường chuẩn: \({\Delta _1}:x =  - 3\) và \({\Delta _2}:x = 3\).

c) Parabol (P): \({y^2} = \frac{1}{2}x\), suy ra \(p = \frac{1}{4}\)

+ Tâm sai \(e = 1\)

+ Tiêu điểm \(F(\frac{1}{8};0)\)

+ Đường chuẩn: \(\Delta :x =  - \frac{1}{8}\)

Vận dụng 2

Quỹ đạo của các vật thể sau đây là những đường conic. Những đường này là elip, parabol hay hypebol.

(Nguồn: https://vi.wikipedia.org/wiki/oumuamud)

Phương pháp giải:

Đường conic có tâm sai e:

+ \(0 < e < 1\) thì conic là đường elip

+ \(e = 1\) thì conic là đường parabol

+ \(e > 1\) thì conic là đường hypebol

Lời giải chi tiết: