HĐ 4
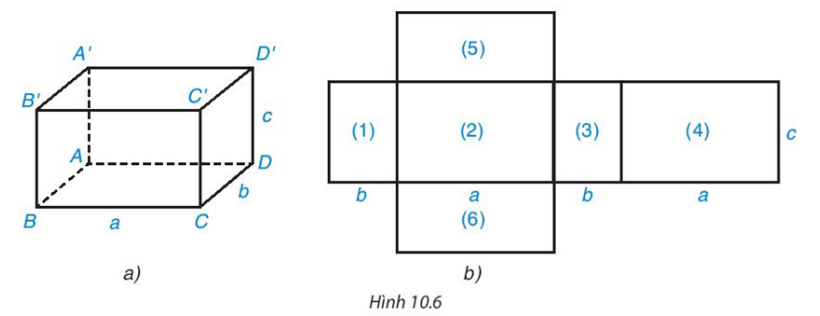
Quan sát hình hộp chữ nhật (H.10.6a) và hình khai triển của nó (H.10.6b). Hãy chỉ ra sự tương ứng giữa các mặt của hình hộp chữ nhật với các hình chữ nhật ở mặt khai triển. Hình chữ nhật nào ở hình khai triển là các mặt bên và mặt đáy?
Phương pháp giải:
Nhìn vào hình vẽ chỉ ra các mặt tương ứng.
(2) và (4) bằng nhau nên là hai mặt lớn đối diện nhau BCC’B’; ADD’A’.
Lời giải chi tiết:
+ Sự tương ứng: (1) – ABB’A’;(2) – BCC’B’; (3) – CDD’C’;(4) – ADD’A’ .
+ Mặt bên : (1), (2), (3), (4)
+ Mặt đáy: (5), (6).
HĐ 5
Tính tổng diện tích các hình chữ nhật (1), (2), (3), (4). So sánh kết quả vừa tìm với tích của chu vi đáy và chiều cao của hình hộp chữ nhật.
Phương pháp giải:
-Diện tích hình chữ nhật = chiều dài x chiều rộng
-Chu vi đáy hình chữ nhật = 2. (chiều dài + chiều rộng )
Lời giải chi tiết:
Diện tích hình chữ nhật (1) = (3) là : bc
Diện tích hình chữ nhật (2) = (4) là ac
\( \Rightarrow \)Tổng diện tích hình chữ nhật (1), (2), (3), (4) = 2ac + 2bc = 2c( a+ b).
Chu vi mặt đáy hình hộp chữ nhật là 2( a+ b)
Độ dài chiều cao của hình hộp chữ nhật là c
\( \Rightarrow \) Tích của chu vi đáy và chiều cao của hình hộp chữ nhật = 2 c(a + b)
\( \Rightarrow \) Tổng diện tích hình chữ nhật (1), (2), (3), (4) = Tích của chu vi đáy và chiều cao của hình hộp chữ nhật = 2 c(a + b)
Luyện tập 1
Bác Tú thuê thợ sơn xung quanh bốn mặt ngoài của thành bể nước có dạng hình hộp chữ nhật có chiều dài 3 m, chiều rộng 2 m, chiều cao 1,5 m với giá 20,000đồng /m2 .Hỏi bác Tú phải chi trả chi phí là bao nhiêu?

Phương pháp giải:
-Tính diện tích xung quanh hình hộp chữ nhật = chu vi đáy x chiều cao.
-Tính chi phí phải trả = diện tích xung quanh x 20000 ( đồng)
Lời giải chi tiết:
Diện tích xung quanh thành bể là :
\(2.\left( {3 + 2} \right).1,5 = 15\left( {{m^2}} \right)\)
Chi phí bác Tú phải trả là :
15. 20000 = 300000 (đồng).
Luyện tập 2
Một hình lập phương có cạnh bằng a cm, diện tích xung quanh bằng \(100c{m^2}\).Hỏi thể tích của hình lập phương đó bằng bao nhiêu?
Phương pháp giải:
-Diện tích xung quanh hình lập phương có cạnh bằng a là \({C_{day}}.chieucao = 4a.a = 4{a^2}\left( {c{m^2}} \right)\)
Thể tích hình lập phương là \({a^3}\left( {c{m^3}} \right)\)
Lời giải chi tiết:
Diện tích xung quanh hình lập phương là: \(S = 4{a^2}\)
\(\begin{array}{l} \Rightarrow 100 = 4{a^2}\\ \Rightarrow {a^2} = 100:4\\ \Rightarrow a = 5\left( {cm} \right)\end{array}\)
Thể tích hình lập phương đó là:
\(V = {a^3} = {5^3} = 125\left( {{m^3}} \right)\)
Vận dụng 2
Một chiếc thùng giữ nhiệt ( H.10.10) có lòng trong có dạng một hình hộp chữ nhật với chiều dài 50 cm, chiều rộng 30 cm, chiều cao 30 cm. Tính dung tích của thùng giữ nhiệt đó.

Phương pháp giải:
Thể tích hình hộp chữ nhật:\(V = a.b.h\)
Lời giải chi tiết:
Thể tích của thùng giữ nhiệt là
50.30.30 = 45 000 ( \(c{m^3}\))
