HĐ Khám phá 3
Cho bất phương trình \(2x - y + 1 < 0\)
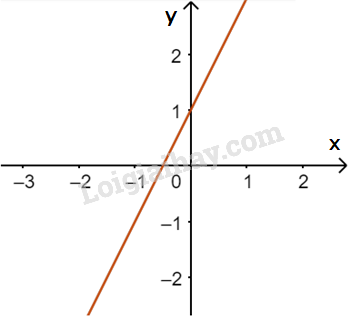
a) Vẽ đường thẳng \(y = 2x + 1\)
b) Các cặp số \(( - 2;0),(0;0),(1;1)\) có là nghiệm của bất phương trình đã cho không?
Lời giải chi tiết:
a) Đường thẳng \(y = 2x + 1\) đi qua điểm \(A(0;1)\) và \(B\left( { - \frac{1}{2};0} \right)\)
b)
Vì \(2.( - 2) - 0 + 1 = - 3 < 0\)nên \(( - 2;0)\) là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.0 - 0 + 1 = 1 > 0\)nên \((0;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Vì \(2.1 - 1 + 1 = 2 > 0\)nên \(( - 2;0)\) không là nghiệm của bất phương trình \(2x - y + 1 < 0\)
Thực hành 3
Biểu diễn miền nghiệm của các bất phương trình sau:
a) \(2x + y - 2 \le 0\)
b) \(x - y - 2 \ge 0\)
Lời giải chi tiết:
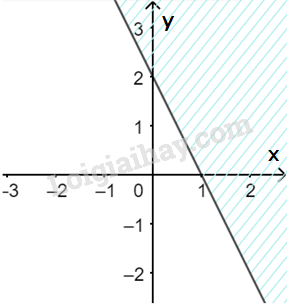
a) Vẽ đường thẳng \(\Delta :2x + y - 2 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(2.0 + 0 - 2 = - 2 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
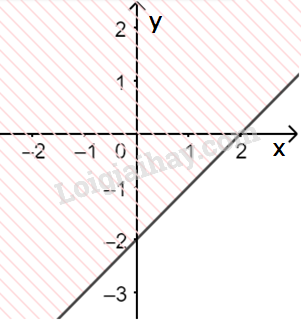
b) Vẽ đường thẳng \(\Delta :x - y - 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {2;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 0 - 2 = - 2 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Vận dụng 2
Biểu diễn miền nghiệm của hai bất phương trình sau trên cùng một mặt phẳng tọa độ Oxy:
a) \(y \ge 2\)
b) \(x \le 4\)
Lời giải chi tiết:
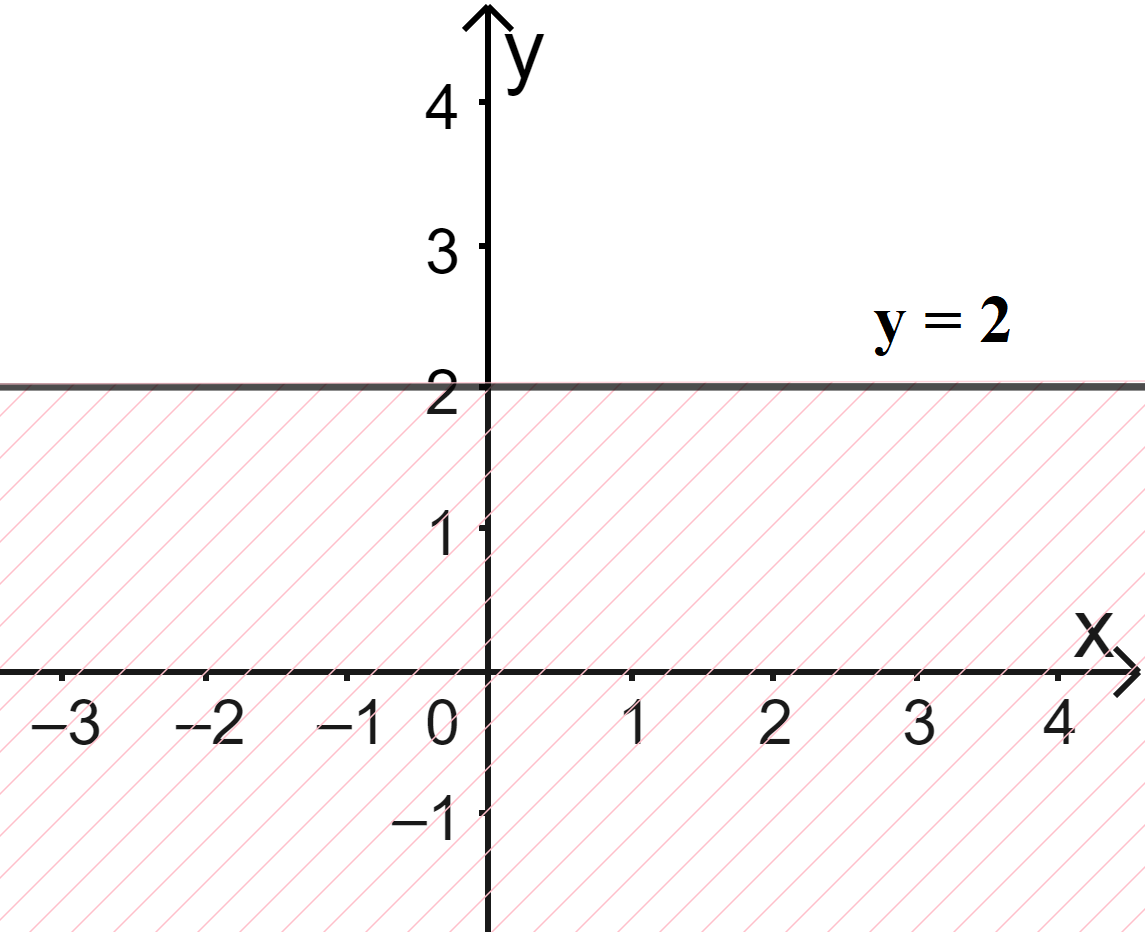
a) Vẽ đường thẳng \(\Delta :y = 2\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \({y_O} = 0 < 2\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa gốc tọa độ O
(miền không gạch chéo trên hình)
b) Vẽ đường thẳng \(\Delta ':x = 4\) đi qua hai điểm \(A'(4;0)\) và \(B'\left( {4;1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta '\) và \({x_O} = 0 < 4\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)