III. Nhân đa thức với đa thức
HĐ 4
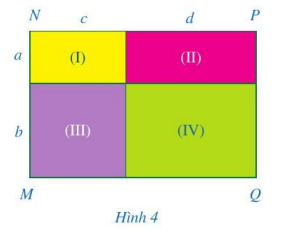
Quan sát hình chữ nhật MNPQ ở Hình 4.
a) Tính diện tích mỗi hình chữ nhật (I), (II), (III), (IV).
b) Tính diện tích của hình chữ nhật MNPQ.
c) So sánh: \((a + b)(c + d)\) và \(ac + ad + bc + bd\).
Phương pháp giải:
a) Diện tích hình chữ nhật bằng chiều dài nhân chiều rộng cùng đơn vị đo.
b) Diện tích hình chữ nhật MNPQ bằng tổng diện tích của 4 hình chữ nhật con.
c) Muốn so sánh \((a + b)(c + d)\) và \(ac + ad + bc + bd\), ta thực hiện phép tính \((a + b)(c + d)\) rồi so sánh.
Lời giải chi tiết:
a)
Diện tích của hình chữ nhật (I) là: \(a.c\).
Diện tích của hình chữ nhật (II) là: \(a.d\).
Diện tích của hình chữ nhật (III) là: \(b.c\).
Diện tích của hình chữ nhật (IV) là: \(b.d\).
b) Diện tích hình chữ nhật MNPQ là: \(ac + ad + bc + bd\).
c) Ta có:
\((a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd\).
Vậy \((a + b)(c + d)\) = \(ac + ad + bc + bd\).
HĐ 5
Cho đa thức \(P(x) = 2x + 3\) và đa thức \(Q(x) = x + 1\).
a) Hãy nhân mỗi đơn thức của đa thức P(x) với từng đơn thức của đa thức Q(x).
b) Hãy cộng các tích vừa tìm được.
Phương pháp giải:
a) Để nhân mỗi đơn thức P(x) với từng đơn thức của đa thức Q(x), trước tiên ta xác định các đơn thức của đa thức P(x), Q(x) rồi sau đó thực hiện phép tính.
b) Cộng các tích vừa tìm được ở phần a).
Lời giải chi tiết:
a)
Các đơn thức của đa thức P(x) là: \(2x;3\).
Các đơn thức của đa thức Q(x) là: \(x;1\).
Tích mỗi đơn thức P(x) với từng đơn thức của đa thức Q(x) lần lượt là: \(2{x^2};2x;3x;3\).
b) Cộng các tích vừa tìm được:
\(2{x^2} + 2x + 3x + 3 = 2{x^2} + 5x + 3\).
LT - VD 3
Tính:
a) \(({x^2} - 6)({x^2} + 6)\);
b) \((x - 1)({x^2} + x + 1)\).
Phương pháp giải:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích lại với nhau.
Lời giải chi tiết:
a) \(\begin{array}{l}({x^2} - 6)({x^2} + 6) = {x^2}({x^2} + 6) + ( - 6).({x^2} + 6) = {x^2}.{x^2} + {x^2}.6) + ( - 6).{x^2} + ( - 6).6\\ = {x^4} + 6{x^2} - 6{x^2} - 36 = {x^4} - 36\end{array}\)
b) \(\begin{array}{l}(x - 1)({x^2} + x + 1) = x({x^2} + x + 1) + ( - 1)({x^2} + x + 1) = x.{x^2} + x.x + x.1 + ( - 1).{x^2} + ( - 1).x + ( - 1).1\\ = {x^3} + {x^2} + x - {x^2} - x - 1 = {x^3} - 1\end{array}\)