Câu hỏi
Kết quả của phép chia 1 cho 9 là số thập phân hữu hạn hay vô hạn tuần hoàn?
Phương pháp giải:
Bước 1: Chia 1 cho 9 để tìm thương dưới dạng số thập phân.
Bước 2: Nhận diện số thập phân đó là hữu hạn hay vô hạn tuần hoàn
Lời giải chi tiết:
Ta có: 1: 9 = 0,1111.... = 0,(1) nên kết quả của phép chia 1 cho 9 là số thập phân vô hạn tuần hoàn.
Luyện tập 1
Viết các phân số \(\frac{1}{4}; - \frac{2}{{11}}\) dưới dạng số thập phân rồi cho biết số nhận được là số thập phân hữu hạn hay vô hạn tuần hoàn.
Chỉ ra chu kì rồi viết gọn nếu đó là số thập phân vô hạn tuần hoàn.
Phương pháp giải:
Thực hiện phép chia tử số cho mẫu số để thu được số thập phân.
Nhận diện số thập phân đó là hữu hạn hay vô hạn tuần hoàn
Lời giải chi tiết:
Ta có: \(\frac{1}{4} = 0,25\). Đây là số thập phân hữu hạn.
\( - \frac{2}{{11}} = - 0,1818....\). Đây là số thập phân vô hạn tuần hoàn. Chu kì của nó là 18. Ta viết \( - \frac{2}{{11}}=-0,(18)\)
Luyện tập 2
Làm tròn số 3,14159 với độ chính xác 0,005.
Phương pháp giải:
+ Bước 1: Xác định hàng làm tròn.
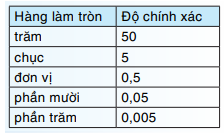
+ Bước 2: Làm tròn theo quy tắc làm tròn số thập phân.
- Đối với chữ số hàng làm tròn:
+ Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;
+Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5
- Đối với chữ số sau hàng làm tròn:
+ Bỏ đi nếu ở phần thập phân;
+ Thay bằng các chữ số 0 nếu ở phần số nguyên
Lời giải chi tiết:
Để làm tròn 3,14159 với độ chính xác 0,005, ta làm tròn đến hàng phần trăm.
Vì chữ số ngay sau phần làm tròn là 1 < 5 nên số 3,14159 làm tròn đến hàng phần trăm là: 3,14
Vận dụng
Ước lượng kết quả phép tính 31,(81).4,9 bằng cách làm tròn hai thừa số đến hàng đơn vị.
Phương pháp giải:
+ Bước 1: Làm tròn 2 thừa số đến hàng đơn vị
+ Bước 2: Tính tích 2 thừa số sau khi làm tròn
Lời giải chi tiết:
Ta có: Làm tròn số 31,(81) đến hàng đơn vị được 32; làm tròn số 4,9 đến hàng đơn vị được 5.
Như vậy, kết quả phép tính 31,(81).4,9 ước lượng được là: 32.5 = 160.
