Câu hỏi 1 :
Một chiếc thuyền chạy ngược dòng trên một đoạn sông thẳng, sau 1 giờ đi được 9km so với bờ. Một đám củi khô trôi trên sông đó, sau 1 phút trôi được 50m so với bờ. Vận tốc của thuyền so với nước là:
- A 12km/h
- B 9km/h
- C 6km/h
- D 3km/h
Đáp án: A
Phương pháp giải:
Công thức cộng vận tốc: \(\overrightarrow {{v_{tb}}} = \overrightarrow {{v_{tn}}} + \overrightarrow {{v_{nb}}} \)
Lời giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{v_{tb}} = \frac{{{s_1}}}{{{t_1}}} = \frac{9}{1} = 9km/h}\\{{v_{nb}} = \frac{{{s_2}}}{{{t_2}}} = \frac{{50}}{{60}} = \frac{5}{6}m/s = 3km/h}\end{array}} \right.\)
Ta có: \(\overrightarrow {{v_{tb}}} = \overrightarrow {{v_{tn}}} + \overrightarrow {{v_{nb}}} \)
Do thuyền chạy ngược dòng sông nên: \({v_{tb}} = {v_{tn}} - {v_{nb}} \Rightarrow {v_{tn}} = {v_{tb}} + {v_{nb}} = 9 + 3 = 12km/h\)
Câu hỏi 2 :
Một xe lửa bắt đầu dời khỏi ga và chuyển động thẳng nhanh dần đều với gia tốc 0,1m/s2. Khoảng thời gian để xe đạt được vận tốc 36km/h là:
- A t = 360s
- B t = 100s
- C t = 300s
- D t = 200s
Đáp án: B
Phương pháp giải:
Công thức tính gia tốc: \(a = \frac{{v - {v_0}}}{t} \Rightarrow t = \frac{{v - {v_0}}}{a}\)
Lời giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{v_0} = 0}\\{a = 0,1m/{s^2}}\\{v = 36km/h = 10m/s}\end{array}} \right.\)
Ta có: \(a = \frac{{v - {v_0}}}{t} \Rightarrow t = \frac{{v - {v_0}}}{a} = \frac{{10 - 0}}{{0,1}} = 100s\)
Câu hỏi 3 :
Một vận động viên môn hốc cây (môn khúc quân cầu) dùng gậy gạt quả bóng để truyền cho nó một tốc độ đầu 10m/s. Hệ số ma sát trượt giữa quả bóng với mặt băng là 0,1. Lấy g = 9,8m/s2. Quãng đường bóng đi được là:
- A 45m
- B 57m
- C 51m
- D 39m
Đáp án: C
Phương pháp giải:
Áp dụng định luật II Niuton: \(\vec F = m\vec a\)
Công thức liên hệ giữa s, v và a: \({v^2} - v_0^2 = 2as \Rightarrow s = \frac{{{v^2} - v_0^2}}{{2a}}\)
Lời giải chi tiết:
Chọn chiều dương là chiều chuyển động của quả bóng.
Bóng chuyển động chậm dần đều dưới tác dụng của lực ma sát nên theo định luât II Niuton ta có:
\(\overrightarrow {{F_{ms}}} = m\vec a{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)\)
Chiếu (*) lên phương chuyển động ta có: \({F_{ms}} = ma\)
\( \Leftrightarrow - \mu N = ma \Leftrightarrow - \mu mg = ma \Rightarrow a = - \mu g = - 0,1.9,8 = - 0,98m/{s^2}\)
Áp dụng công thức liên hệ giữa s, v và a ta có: \({v^2} - v_0^2 = 2as \Rightarrow s = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{{0^2} - {{10}^2}}}{{2.\left( { - 0,98} \right)}} = 51m\)
Câu hỏi 4 :
Một chiếc xe đạp đang chạy với tốc độ 36km/h thì tài xế hãm phanh, xe chuyển động thẳng chậm dần đều rồi đứng lại sau 5s. Quãng đường xe chạy được trong giây cuối cùng là:
- A 2m
- B 2,5m
- C 1,25m
- D 1m
Đáp án: D
Phương pháp giải:
Công thức tính gia tốc: \(a = \frac{{v - {v_0}}}{t}\)
Phương trình vận tốc: \(v = {v_0} + at = 10 - 2t{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\)
Công thức liên hệ giữa s, v và a: \({v^2} - v_0^2 = 2as \Rightarrow s = \frac{{{v^2} - v_0^2}}{{2a}}\)
Lời giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{v_0} = 36km/h = 10m/s}\\{t = 5s}\\{{v_d} = 0}\end{array}} \right.\)
Gia tốc của xe là: \(a = \frac{{{v_d} - {v_0}}}{t} = \frac{{0 - 10}}{5} = - 2m/{s^2}\)
Phương trình vận tốc của xe: \(v = {v_0} + at = 10 - 2t{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\)
Vận tốc của xe lúc t = 4s là: \(v = 10 - 2.4 = 2{\mkern 1mu} {\mkern 1mu} \left( {m/s} \right)\)
Áp dụng công thức liên hệ giữa s, v và a cho 2 vị trí (lúc t = 4s đến khi dừng lại) ta có:
\(v_d^2 - {v^2} = 2as \Rightarrow s = \frac{{v_d^2 - {v^2}}}{{2a}} = \frac{{{0^2} - {2^2}}}{{2.\left( { - 2} \right)}} = 1m\)
Câu hỏi 5 :
Chọn đáp án đúng. Trong chuyển động ném ngang, chuyển động của chất điểm là:
- A Chuyển động thẳng đều.
- B Chuyển động rơi tự do.
- C Chuyển động thẳng đều theo phương ngang, rơi tự do theo phương thẳng đứng.
- D Chuyển động thẳng biến đổi đều.
Đáp án: C
Phương pháp giải:
Phân tích chuyển động ném ngang thành 2 chuyển động trên Ox và Oy.
Trên Ox: Vật chuyển động thẳng đều với vận tốc: \({v_x} = {v_0}\)
Trên Oy: Vật chuyển động rơi tự do.
Lời giải chi tiết:
Trong chuyển động ném ngang, chuyển động của chất điểm là: Chuyển động thẳng đều theo phương ngang, rơi tự do theo phương thẳng đứng.
Câu hỏi 6 :
Chọn đáp án đúng:
- A Ngẫu lực là hệ hai lực song song, cùng chiều, có độ lớn bằng nhau và cùng tác dụng vào một vật.
- B Ngẫu lực là hệ hai lực song song, ngược chiều, có độ lớn bằng nhau và cùng tác dụng vào một vật.
- C Ngẫu lực là hệ hai lực song song, ngược chiều, có độ lớn bằng nhau và tác dụng vào hai vật.
- D Ngẫu lực là hệ hai lực song song, có độ lớn bằng nhau và cùng tác dụng vào một vật.
Đáp án: B
Phương pháp giải:
Hệ hai lực song song, ngược chiều có độ lớn bằng nhau và cùng tác dụng vào một vật gọi là ngẫu lực.
Lời giải chi tiết:
Ngẫu lực là hệ hai lực song song, ngược chiều, có độ lớn bằng nhau và cùng tác dụng vào một vật.
Câu hỏi 7 :
Chọn đáp số đúng. Hai lực đồng quy có độ lớn là 9N và 12N. Giá trị nào có thể là độ lớn của hợp lực:
- A 25N
- B 1N
- C 2N
- D 15N
Đáp án: D
Phương pháp giải:
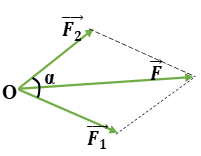
Áp dụng quy tắc hình bình hành: \(\vec F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)
Độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \)
Vì \({0^0}\; \le \alpha \le {180^0}\; \Rightarrow \left| {{F_1}\; - {F_2}} \right| \le F \le {F_1}\; + {F_2}\)
Lời giải chi tiết:
Công thức xác định độ lớn của hợp lực: \(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \)
Ta có: \(\left| {{F_1}\; - {F_2}} \right| \le F \le {F_1}\; + {F_2} \Leftrightarrow 3 \le F \le 21\)\( \Rightarrow \) Vậy 15N là giá trị có thể là độ lớn của hợp lực
Câu hỏi 8 :
Tần số của đầu kim phút là:
- A 60 phút
- B \(\frac{1}{{60}}Hz\)
- C \(3600{s^{ - 1}}\)
- D \(\frac{1}{{3600}}{s^{ - 1}}\)
Đáp án: D
Phương pháp giải:
Tần số: \(f = \frac{1}{T}\)
Chu kì T là thời gian vật quay hết 1 vòng.
Lời giải chi tiết:
Chu kì của kim phút là: \(T = 1h = 3600s\)
Tần số của kim phút là: \(f = \frac{1}{T} = \frac{1}{{3600}}{s^{ - 1}}\)
Câu hỏi 9 :
Phải treo một vật có trọng lượng bằng bao nhiêu vào lò xo có độ cứng k = 100N/m để nó dãn được 10cm?
- A 100N
- B 1000N
- C 1N
- D 10N
Đáp án: D
Phương pháp giải:
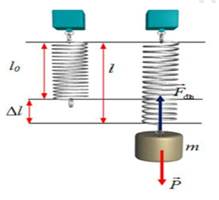
Công thức tính độ lớn lực đàn hồi: \({F_{dh}} = k.\Delta l\)
Trọng lực: \(P = mg\)
Khi vật nặng cân bằng thì: \(P = {F_{dh}}\)
Lời giải chi tiết:
Vật nặng chịu tác dụng của: Lực đàn hồi: \({F_{dh}} = k.\Delta l\); Trọng lực: \(P = mg\)
Khi vật cân bằng thì: \(\overrightarrow {{F_{dh}}} + \vec P = \vec 0 \Rightarrow P = {F_{dh}} = k.\Delta l = 100.0,1 = 10N\)
Câu hỏi 10 :
Chọn đáp án đúng. Giới hạn đàn hồi của vật là giới hạn trong đó vật:
- A còn giữ được tính đàn hồi
- B không còn giữ được tính đàn hồi
- C bị biến dạng dẻo
- D bị mất tính đàn hồi
Đáp án: A
Lời giải chi tiết:
Giới hạn đàn hồi của vật là giới hạn trong đó vật còn giữ được tính đàn hồi.
Câu hỏi 11 :
Để xác định sự thay đổi vị trí của một chất điểm theo thời gian, người ta dùng:
- A Phương trình toạ độ theo thời gian
- B Công thức đường đi
- C Công thức vận tốc
- D Hệ toạ độ
Đáp án: A
Lời giải chi tiết:
Để xác định sự thay đổi vị trí của một chất điểm theo thời gian người ta dùng phương trình toạ độ theo thời gian.
Câu hỏi 12 :
Khi ô tô đang chạy với vận tốc 10m/s trên đoạn đường thẳng thì người lái xe hãm phanh và ô tô chuyển động chậm dần đều. Cho tới khi dừng hẳn lại thì ô tô đã chạy thêm được 100m. Gia tốc của ô tô là:
- A \(a = 0,2m/{s^2}\)
- B \(a = - 0,5m/{s^2}\)
- C \(a = 0,5m/{s^2}\)
- D \(a = - 0,2m/{s^2}\)
Đáp án: B
Phương pháp giải:
Công thức liên hệ giữa s, v và a: \({v^2} - v_0^2 = 2as \Rightarrow a = \frac{{{v^2} - v_0^2}}{{2s}}\)
Lời giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{v = 10m/s}\\{v = 0}\\{s = 100m}\end{array}} \right.\)
Áp dụng công thức liên hệ giữa s, v và a ta có: \({v^2} - v_0^2 = 2as \Rightarrow a = \frac{{{v^2} - v_0^2}}{{2s}} = \frac{{0 - {{10}^2}}}{{2.100}} = - 0,5m/{s^2}\)
Câu hỏi 13 :
Ở trên mặt đất một vật có trọng lượng 9N. Khi chuyển vật tới một điểm cách tâm Trái Đất 3R (R là bán kính Trái Đất) thì nó có trọng lượng bằng bao nhiêu?
- A 3N
- B 9N
- C \(\frac{9}{{16}}N\)
- D 1N
Đáp án: D
Phương pháp giải:
Trọng lượng của một vật trên mặt đất: \(P = G.\frac{{mM}}{{{R^2}}}\)
Trọng lượng của một vật ở độ cao h: \({P_h} = G.\frac{{mM}}{{{{\left( {R + h} \right)}^2}}}\)
Lời giải chi tiết:
Vật ở trên mặt đất: \(P = G.\frac{{mM}}{{{R^2}}} = 9N\)
Khi chuyển vật tới một điểm cách tâm Trái Đất 3R: \({P_h} = G.\frac{{mM}}{{{{\left( {3R} \right)}^2}}} = \frac{1}{9}G.\frac{{mM}}{{{R^2}}} = \frac{P}{9} = \frac{9}{9} = 1N\)
Câu hỏi 14 :
Một lực F truyền cho một vật khối lượng \({m_1}\) một gia tốc 6m/s2, truyền cho \({m_2}\) gia tốc 3m/s2. Lực F truyền cho \({m_1}\; + {m_2}\;\) một gia tốc là:
- A \(3m/{s^2}\)
- B \(4,5m/{s^2}\)
- C \(2m/{s^2}\)
- D \(9m/{s^2}\)
Đáp án: C
Phương pháp giải:
Áp dụng định luật II Niuton ta có: \(F = ma \Rightarrow m = \frac{F}{a}\)
Lời giải chi tiết:
Theo bài ra ta có: \(\left\{ {\begin{array}{*{20}{l}}{{m_1} = \frac{F}{{{a_1}}}}\\{{m_2} = \frac{F}{{{a_2}}}}\\{{m_1} + {m_2} = \frac{F}{a}}\end{array}} \right. \Rightarrow \frac{F}{{{a_1}}} + \frac{F}{{{a_2}}} = \frac{F}{a} \Leftrightarrow \frac{1}{6} + \frac{1}{3} = \frac{1}{a} \Rightarrow \frac{1}{a} = \frac{1}{2} \Rightarrow a = 2m/{s^2}\)
Câu hỏi 15 :
Hoà nói với Bình: ‘’Mình đi mà hoá ra đứng, cậu đứng mà hoá ra đi’’. Trong câu nói này, Hoà đã chọn vật làm mốc là gì?
- A Bình
- B Hoà
- C Cả Hoà và Bình
- D Mặt đất
Đáp án: B
Phương pháp giải:
Chuyển động của một vật là sự thay đổi vị trí của vật đó so với các vật khác theo thời gian.
Chuyển động và đứng yên có tính tương đối tuỳ thuộc vào vật được chọn làm mốc
Lời giải chi tiết:
Hoà nói với Bình: ‘’Mình đi mà hoá ra đứng, cậu đứng mà hoá ra đi’’. Trong câu nói này, Hoà đã chọn Hoà làm vật mốc
Câu hỏi 16 :
Một người gánh một thùng gạo nặng 250N và một thùng ngô 150N trên một đòn gánh. Hỏi vai người chịu một lực bằng bao nhiêu? Bỏ qua trọng lượng của đòn gánh:
- A Chịu lực 500N
- B Chịu lực 400N
- C Chịu lực 200N
- D Chịu lực 100N
Đáp án: B
Phương pháp giải:
Sử dụng quy tắc tổng hợp hai lực song song cùng chiều:
+ Hợp lực của hai lực song song cùng chiều là một lực song song, cùng chiều và có độ lớn bằng tổng các độ lớn của hai lực ấy.
+ Giá của hợp lực chia khoảng cách giữa hai giá của hai lực song song thành những đoạn tỉ lệ nghịch với độ lớn của hai lực ấy.
Lời giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{{F_1} = 250N}\\{{F_2} = 150N}\end{array}} \right.\)
Vai người chịu một lực: \(F = {F_1} + {F_2} = 250 + 150 = 400N\)
Câu hỏi 17 :
Hòn bi A có khối lượng lớn gấp đôi hòn bi B. Cùng một lúc từ độ cao h, bi A được thả rơi còn bi B được ném theo phương ngang. Bỏ qua sức cản của không khí. Hãy cho biết câu nào dưới đây đúng:
- A A chạm đất trước
- B A chạm đất sau
- C Cả hai chạm đất cùng lúc
- D Phụ thuộc vào vận tốc ném bi B
Đáp án: C
Phương pháp giải:
Thời gian chuyển động của vật bị ném ngang bằng thời gian rơi tự do của vật được thả từ cùng một độ cao: \(t = \sqrt {\frac{{2h}}{g}} \)
Lời giải chi tiết:
Ta có: Thời gian chuyển động của vật bị ném ngang bằng thời gian rơi tự do của vật được thả từ cùng một độ cao.
Hòn bi A có khối lượng lớn gấp đôi hòn bi B. Cùng một lúc từ độ cao h, bi A được thả rơi còn bi B được ném theo phương ngang. Bỏ qua sức cản của không khí thì hai vật chạm đất cùng lúc.
Câu hỏi 18 :
Nếu hợp lực tác dụng lên một vật là lực không đổi theo thời gian thì vật đó sẽ thực hiện chuyển động:
- A Chậm dần đều hoặc nhanh dần đều
- B Thẳng đều
- C Nhanh dần đều theo phương tác dụng lực
- D Chậm dần đều theo phương tác dụng lực
Đáp án: A
Phương pháp giải:
Định luật II Niuton: Gia tốc của một vật cùng hướng với lực tác dụng lên vật. Độ lớn của gia tốc tỉ lệ thuận với độ lớn của lực và tỉ lệ nghịch với khối lượng của vật: \(\vec a{\rm{\;}} = \frac{{\vec F}}{m}\)
Lời giải chi tiết:
Nếu hợp lực tác dụng lên một vật là lực không đổi theo thời gian thì vật đó sẽ thực hiện chuyển động chậm dần đều hoặc nhanh dần đều.
Câu hỏi 19 :
Momen lực của một lực đối với trục quay là bao nhiêu nếu độ lớn của lực là 5,5N và cánh tay đòn là 2 mét?
- A 11N/m
- B 275N.m
- C 11N
- D 11N.m
Đáp án: D
Phương pháp giải:
Công thức tính momen lực: \(M = F.d\)
Lời giải chi tiết:
Momen của lực đối với trục quay là: \(M = F.d = 5,5.2 = 11N.m\)
Câu hỏi 20 :
Một vật rơi tự do từ độ cao 80m. Lấy \(g = 10m/{s^2}\). Quãng đường vật rơi được trong 2s và trong giây thứ 2 là:
- A 45m và 20m
- B 20m và 15m
- C 20m và 35m
- D 20m và 10m
Đáp án: B
Phương pháp giải:
Quãng đường vật rơi trong n giây: \({s_{t = n}} = \frac{1}{2}g.{n^2}\)
Quãng đường vật rơi trong giây thứ n: \({s_n} = {s_{t = n}} - {s_{t = n - 1}} = \frac{1}{2}g.{n^2} - \frac{1}{2}g.{\left( {n - 1} \right)^2}\)
Lời giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{h = 80m}\\{g = 10m/{s^2}}\end{array}} \right.\)
Quãng đường vật rơi trong 2s là: \({s_{t = 2}} = \frac{1}{2}g.{t^2} = \frac{1}{2}{.10.2^2} = 20m\)
Quãng đường vật rơi trong giây thứ hai là: \({s_2} = {s_{t = 2}} - {s_{t = 1}} = \frac{1}{2}{.10.2^2} - \frac{1}{2}{.10.1^2} = 15m\)
Câu hỏi 21 :
Trong các yếu tố sau, yếu tố nào không có tính tương đối:
- A quãng đường đi được
- B quỹ đạo
- C toạ độ
- D vận tốc
Đáp án: A
Lời giải chi tiết:
Quãng đường đi được không có tính tương đối
Câu hỏi 22 :
Một người có khối lượng 50kg hút Trái Đất với một lực bằng bao nhiêu? Lấy \(g = 9,81m/{s^2}\).
- A 490,5N
- B 50N
- C 49,05N
- D 500N
Đáp án: A
Phương pháp giải:
Trọng lực của một vật là lực hấp dẫn giữa Trái Đất và vật đó
Lời giải chi tiết:
Một người khối lượng 50kg hút Trái Đất với một lực bằng: \(P = m.g = 9,81.50 = 490,5N\)
Câu hỏi 23 :
Một máy bay bay ngang với tốc độ 150m/s, ở độ cao 490m thì thả một gói hàng xuống đất. Lấy \(g = 9,8m/{s^2}\). Tầm bay xa của gói hàng là:
- A 7500m
- B 15000m
- C 1500m
- D 1000m
Đáp án: C
Phương pháp giải:
Tầm ném xa: \(L = {v_0}t = {v_0}.\sqrt {\frac{{2h}}{g}} \)
Lời giải chi tiết:
Gói hàng thả từ máy bay được coi như vật ném ngang từ độ cao h = 490m với vận tốc ban đầu\({v_0} = 150m/s\)
Tầm bay xa của gói hàng là: \(L = {v_0}t = {v_0}.\sqrt {\frac{{2h}}{g}} {\rm{\;}} = 150.\sqrt {\frac{{2.490}}{{9,8}}} {\rm{\;}} = 1500m\)
Câu hỏi 24 :
Phương trình chuyển động của một chất điểm dọc theo trục Ox có dạng: \(x = 5 + 60t\) (x đo bằng km và t đo bằng giờ). Chất điểm đó xuất phát từ điểm nào và chuyển động với vận tốc bằng bao nhiêu?
- A Từ điểm M cách O là 5km, với vận tốc 60km/h
- B Từ điểm M cách O là 5km, với vận tốc 5km/h
- C Từ điểm O với vận tốc 5km/h
- D Từ điểm O với vận tốc 60km/h
Đáp án: A
Phương pháp giải:
Phương trình chuyển động thẳng đều: \(x = {x_0} + {v_0}t\)
Lời giải chi tiết:
Phương trình chuyển động tổng quát: \(x = {x_0} + {v_0}t\)
Phương trình chuyển động bài cho: \(x = 5 + 60t\)
Đồng nhất hai phương trình ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_0} = 5km}\\{{v_0} = 60km/h}\end{array}} \right.\)
Vậy chất điểm xuất phát từ điểm M cách O là 5km, với vận tốc 60km/h.
Câu hỏi 25 :
Một quả cầu đồng chất có khối lượng 3kg được treo vào tường nhờ một sợi dây. Dây làm với tường một góc \(\alpha = {20^0}\) (hình vẽ). Bỏ qua ma sát chỗ tiếp xúc của quả cầu với tường. Lấy \(g = 10m/{s^2}\). Lực căng T của dây là:
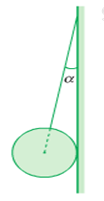
- A 82,42N
- B 87,71N
- C 78N
- D 31,92N
Đáp án: D
Phương pháp giải:
Điều kiện cân bằng của một chất điểm là hợp lực của các lực tác dụng lên nó phải bằng 0:\(\vec F{\rm{\;}} = \overrightarrow {{F_1}} {\rm{\;}} + \overrightarrow {{F_2}} {\rm{\;}} + ... = \vec 0\)
Lời giải chi tiết:
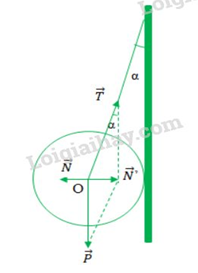
Ta có: \(m = 3kg;\;g = 9,8m/{s^2};\alpha {\rm{\;}} = {20^0}\)
Lực tác dụng lên quả cầu được biểu diễn trên hình vẽ:
Khi hệ cân bằng ta có: \(\vec P{\rm{\;}} + \vec T{\rm{\;}} + \vec N{\rm{\;}} = \vec 0{\mkern 1mu} \Leftrightarrow \vec P{\rm{\;}} + \vec T{\rm{\;}} = {\rm{\;}} - \vec N{\rm{\;}} \Leftrightarrow \vec P{\rm{\;}} + \vec T{\rm{\;}} = \vec N'\)
Xét tam giác N’OT vuông tại N’ ta có:
\(\cos \alpha {\rm{\;}} = \frac{P}{T} \Rightarrow T = \frac{P}{{\cos \alpha }} = \frac{{mg}}{{\cos \alpha }} = \frac{{3.10}}{{\cos 20}} = 31,92N\)
Câu hỏi 26 :
Các dạng cân bằng của vật rắn là:
- A Cân bằng bền, cân bằng không bền, cân bằng phiếm định
- B Cân bằng bền, cân bằng phiếm định
- C Cân bằng không bền, cân bằng phiếm định
- D Cân bằng bền, cân bằng không bền
Đáp án: A
Lời giải chi tiết:
Các dạng cân bằng của vật rắn là: Cân bằng bền, cân bằng không bền, cân bằng phiếm định.
Câu hỏi 27 :
Biểu thức tính độ lớn của lực hướng tâm là:
- A \({F_{ht}} = k.\left| {\Delta l} \right|\)
- B \({F_{ht}} = mg\)
- C \({F_{ht}} = m.{\omega ^2}.r\)
- D \({F_{ht}} = \mu mg\)
Đáp án: C
Phương pháp giải:
Công thức của lực hướng tâm: \({F_{ht}} = \frac{{m{v^2}}}{r} = m.{\omega ^2}.r\)
Lời giải chi tiết:
Biểu thức tính độ lớn của lực hướng tâm là:\({F_{ht}} = m.{\omega ^2}.r\)
Câu hỏi 28 :
Hệ số ma sát giữa hai mặt tiếp xúc sẽ thay đổi như thế nào nếu lực ép hai mặt đó tăng lên:
- A Không biết được
- B Không thay đổi
- C Tăng lên
- D Giảm đi
Đáp án: B
Phương pháp giải:
Hệ số ma sát trượt phụ thuộc vào vật liệu và tình trạng của hai mặt tiếp xúc
Lời giải chi tiết:
Hệ số ma sát trượt không phụ thuộc vào lực ép hai mặt tiếp xúc. Do đo khi thay đổi lực ép hai mặt đó thì hệ số ma sát giữa hai mặt tiếp xúc không thay đổi.
Câu hỏi 29 :
Một lốp ô tô chứa không khí ở \(5{\rm{ }}bar\) và \({25^0}C\) . Khi xe chạy, lốp xe nóng lên làm cho nhiệt độ không khí trong lốp tăng lên tới \({50^0}C\). Lúc này áp suất trong lốp xe bằng:
- A \(5,42{\rm{ }}bar\)
- B \(3,3{\rm{ }}bar\;\)
- C \(4{\rm{ }}bar\)
- D \(5,6{\rm{ }}bar\)
Đáp án: A
Phương pháp giải:
Định luật Sác - lơ: Trong quá trình đẳng tích của một lượng khí nhất định, áp suất tỉ lệ thuận với nhiệt độ tuyệt đối.
Hệ thức: \(p\~T \Rightarrow \frac{p}{T} = const\)
Lời giải chi tiết:
Áp dụng định luật Saclơ cho hai trạng thái 1 và trạng thái 2 ta được:
\(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \Rightarrow {p_2} = \frac{{{p_1}{T_2}}}{{{T_1}}} = \frac{{5.323}}{{298}} = 5,42Pa\)
Câu hỏi 30 :
Khi khoảng cách giữa các phân tử rất nhỏ, thì giữa các phân tử
- A chỉ có lực hút
- B có cả lực hút và lực đẩy, nhưng lực đẩy lớn hơn lực hút
- C chỉ có lực đẩy
- D có cả lực hút và lực đẩy, nhưng lực đẩy nhỏ hơn lực hút
Đáp án: B
Phương pháp giải:
Lí thuyết về lực tương tác phân tử: Khi khoảng cách giữa các phân tử nhỏ thì lực đẩy mạnh hơn lực hút. Khi khoảng cách giữa các phân tử lớ thì lực hút mạnh hơn lực đẩy. Khi khoảng cách giữa các phân tử rất lớn (lớn hơn rất nhiều lần kích thước phân tử) thì lực tương tác giữa chúng coi như không đáng kể.
Lời giải chi tiết:
Khi khoảng cách giữa các phân tử rất nhỏ, thì giữa các phân tử có cả lực hút và lực đẩy, nhưng lực đẩy lớn hơn lực hút.
Câu hỏi 31 :
Trong quá trình chất khí nhận nhiệt và sinh công thì A và Q trong biểu thức \(\Delta U = Q + A\;\) phải có giá trị nào sau đây?
- A \(Q < 0,A > 0\)
- B \(Q > 0,{\rm{ }}A < 0\)
- C \(Q > 0,A > 0\)
- D \(Q < 0,{\rm{ }}A < 0\)
Đáp án: B
Phương pháp giải:
Nguyên lí I của nhiệt động lực học: Độ biến thiên nội năng của vật bằng tổng công và nhiệt lượng mà vật nhận được.
Ta có: \(\Delta U = A + Q\)
Với quy ước về dấu:
+ \(Q > 0\) : Hệ nhận nhiệt lượng; \(Q < 0\): Hệ truyền nhiệt lượng
+ \(A > 0\): Hệ nhận công; \(A < 0\): Hệ thực hiện công
Lời giải chi tiết:
Hệ nhận nhiệt \( \Rightarrow Q > 0\) và sinh công \( \Rightarrow A < 0\)
\( \Leftarrow \) Trong quá trình chất khí nhận nhiệt và sinh công thì A và Q trong biểu thức \(\Delta U = Q + A\;\) phải có giá trị \(Q > 0,{\rm{ }}A < 0\).
Câu hỏi 32 :
Thực hiện công \(100J\) để nén khí trong xylanh và khí truyền ra môi trường một nhiệt lượng 20 J. Kết luận nào sau đây là đúng?
- A Nội năng của khí tăng \(80J\)
- B Nội năng của khí tăng \(120J\)
- C Nội năng của khí giảm \(80J\)
- D Nội năng của khí giảm \(120J\)
Đáp án: D
Phương pháp giải:
Nguyên lí I của nhiệt động lực học: Độ biến thiên nội năng của vật bằng tổng công và nhiệt lượng mà vật nhận được.
Ta có: \(\Delta U = A + Q\)
Với quy ước về dấu:
+ \(Q > 0\) : Hệ nhận nhiệt lượng; \(Q < 0\): Hệ truyền nhiệt lượng
+ \(A > 0\): Hệ nhận công; \(A < 0\): Hệ thực hiện công
Lời giải chi tiết:
Theo nguyên lí I nhiệt động lực học \(\Delta U = A + Q\)
Thực hiện công \( \Rightarrow A < 0\), truyền nhiệt lượng \( \Rightarrow Q < 0\)
\( \Rightarrow \Delta U = Q + A = - 20 + \left( { - 100} \right) = - 120J\) \( \Rightarrow \)Nội năng giảm \(120J\)
Câu hỏi 33 :
Đặc điểm và tính chất nào dưới đây không đúng về chất rắn kết tinh?
- A Có cấu trúc tinh thể
- B Có nhiệt độ nóng chảy xác định
- C Có dạng hình học xác định
- D Có nhiệt độ nóng chảy không xác định.
Đáp án: D
Phương pháp giải:
+ Các chất rắn được phân thành hai loại: kết tinh và vô định hình.
+ Chất rắn kết tinh có cấu trúc tinh thể, do đó có dạng hình học và nhiệt độ nóng chảy xác định.
+ Chất rắn kết tinh có thể là chất đơn tinh thể hoặc chất đa tinh thể. Chất rắn đơn tinh thể có tính dị hướng, còn chất rắn đa tinh thể có tính đẳng hướng.
+ Chất rắn vô định hình không có cấu trúc tinh thể, do đó không có dạng hình học xác định, không có nhiệt độ nóng chảy (hoặc đông đặc) xác định và có tính đẳng hướng.
Lời giải chi tiết:
Chất rắn kết tinh có nhiệt độ nóng chảy (hoặc đông đặc) xác định.
\( \Rightarrow \) Phát biểu sai là: Có nhiệt độ nóng chảy không xác định.
Câu hỏi 34 :
Kéo một xe goòng bằng một sợi dây cáp với một lực bằng \(150N\). Góc giữa dây cáp và mặt phẳng ngang bằng \({30^0}\). Công của lực tác dụng lên xe để xe chạy được \(200m\) có giá trị
- A \(51900J\)
- B \(30000J\)
- C \(15000J\)
- D \(25980J\)
Đáp án: D
Phương pháp giải:
Công thức tính công: \(A = F.s.cos\alpha ;\,\alpha = \left( {\overrightarrow F ;\overrightarrow s } \right)\)
Lời giải chi tiết:
Công của lực tác dụng lên xe có giá trị: \(A = F.s.cos\alpha = 150.200.cos{30^0} = 25980J\)
Câu hỏi 35 :
Người ta thả rơi tự do một vật \(400g\) từ điểm B cách mặt đất \(20m\). Bỏ qua ma sát, lấy \(g = 10m/{s^2}\). Cơ năng của vật tại C cách B một đoạn \(5m\) là
- A \(20J\)
- B \(60J\)
- C \(40J\)
- D \(80J\)
Đáp án: D
Phương pháp giải:
+ Cơ năng của vật chuyển động trong trọng trường: \(W = {W_d} + {W_t} = \frac{1}{2}m{v^2} + mgz\)
+ Định luật bảo toàn cơ năng: Khi một vật chuyển động trong trọng trường chỉ chịu tác dụng của trọng lực thì cơ năng của vật là một đại lượng bảo toàn.
Lời giải chi tiết:
Vật thả rơi tự do có vận tốc ban đầu bằng 0.
Tại B có: \(\left\{ \begin{array}{l}m = 400g = 0,4kg\\h = 20m\\v = 0\\g = 10m/{s^2}\end{array} \right.\)
Cơ năng tại B: \({W_B} = {W_d} + {W_t} = \frac{1}{2}m{v^2} + mgh = 0 + 0,4.10.20 = 80J\)
Bỏ qua ma sát \( \Rightarrow \) Cơ năng được bảo toàn nên: \({W_C} = {W_B} = 80J\)
Câu hỏi 36 :
Một lò xo có độ cứng \(100N/m\), một đầu cố định, đầu kia gắn với vật nhỏ. Khi lò xo bị nén \(4cm\) thì thế năng đàn hồi của hệ là
- A \(800J\)
- B \(0,08J\)
- C \(8N.m\)
- D \(8J\)
Đáp án: B
Phương pháp giải:
Thế năng đàn hồi: \({W_t} = \frac{1}{2}k{\left( {\Delta l} \right)^2}\)
Lời giải chi tiết:
Thế năng đàn hồi của hệ khi lò xo bị nén 4cm là: \({W_t} = \frac{1}{2}.k{\left( {\Delta l} \right)^2} = \frac{1}{2}.100.0,042 = 0,08J\)
Câu hỏi 37 :
Nếu áp suất của một lượng khí lí tưởng tăng \({2.10^5}Pa\) thì thể tích biến đổi 3 lít. Nếu áp suất của lượng khí đó tăng \({5.10^5}Pa\) thì thể tích biến đổi 5 lít. Biết nhiệt độ không đổi, áp suất và thể tích ban đầu của khí là:
- A \({2.10^5}Pa,{\rm{ }}8l\'i t\)
- B \({4.10^5}Pa,{\rm{ }}12l\'i t\;\)
- C \({4.10^5}Pa,{\rm{ }}9l\'i t\)
- D \({2.10^5}Pa,\,\,12l\'i t\)
Đáp án: C
Phương pháp giải:
Định luật Bô-lơ - Ma-ri-ốt: Trong quá trình đẳng nhiệt của một lượng khí nhất định, áp suất tỉ lệ nghịch với thể tích.
Hệ thức: \(p\~\frac{1}{V} \Rightarrow \;PV = const\)
Lời giải chi tiết:
Trạng thái 1: \(\left\{ \begin{array}{l}{p_1}\\{V_1}\\T\end{array} \right.\)
Trạng thái 2: \(\left\{ \begin{array}{l}{p_2} = {p_1} + {2.10^5}\\{V_2} = {V_1} - 3\\T\end{array} \right.\)
Trạng thái 3: \(\left\{ \begin{array}{l}{p_3} = {p_1} + {5.10^5}\\{V_3} = {V_1} - 5\\T\end{array} \right.\)
Áp dụng định luật Bôilơ Mariốt cho trạng thái 1 và 2 ta được:
\(\begin{array}{l}{p_1}{V_1} = \left( {{p_1} + {{2.10}^5}} \right).\left( {{V_1} - 3} \right)\\ \Leftrightarrow {p_1}{V_1} = {p_1}{V_1} - 3{p_1} + {2.10^5}{V_1} - {6.10^5} \Leftrightarrow 3{p_1} - {2.10^5}{V_1} = {6.10^5}\,\,\,\,\,\left( 1 \right)\end{array}\)
Áp dụng định luật Bôilơ Mariốt cho trạng thái 1 và 3 ta được:
\(\begin{array}{l}{p_1}{V_1} = \left( {{p_1} + {{5.10}^5}} \right).\left( {{V_1} - 5} \right)\\ \Leftrightarrow {p_1}{V_1} = {p_1}{V_1} - 5{p_1} + {5.10^5}{V_1} - {25.10^5} \Leftrightarrow 5{p_1} - {5.10^5}{V_1} = {25.10^5}\,\,\,\,\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}{p_1} = {4.10^5}Pa\\{V_1} = 9l\end{array} \right.\)
Câu hỏi 38 :
Dưới áp suất \({10^5}Pa\) một lượng khí có thể tích là 10 lít. Nếu nhiệt độ được giữ không đổi và áp suất tăng lên \(1,{25.10^5}Pa\) thì thể tích là
- A 7 lít
- B 8 lít
- C 9 lít
- D 10 lít
Đáp án: B
Phương pháp giải:
Định luật Bô-lơ - Ma-ri-ốt: Trong quá trình đẳng nhiệt của một lượng khí nhất định, áp suất tỉ lệ nghịch với thể tích.
Hệ thức: \(p\~\frac{1}{V} \Rightarrow \;PV = const\)
Lời giải chi tiết:
Áp dụng định luật Boilo – Mariot ta có: \({p_1}{V_1} = {p_2}{V_2} \Rightarrow {V_2} = \frac{{{p_1}{V_1}}}{{{p_2}}} = \frac{{{{10}^5}.10}}{{1,{{25.10}^5}}} = 8l\)
Câu hỏi 39 :
Phân loại chất rắn theo các cách nào dưới đây?
- A Chất rắn kết tinh và chất rắn vô định hình
- B Chất rắn đơn tinh thể và chất rắn vô định hình
- C Chất rắn đơn tinh thể và chất rắn đa tinh thể
- D Chất rắn đa tinh thể và chất rắn vô định hình.
Đáp án: A
Phương pháp giải:
+ Các chất rắn được phân thành hai loại: kết tinh và vô định hình.
+ Chất rắn kết tinh có cấu trúc tinh thể, do đó có dạng hình học và nhiệt độ nóng chảy xác định.
+ Chất rắn kết tinh có thể là chất đơn tinh thể hoặc chất đa tinh thể. Chất rắn đơn tinh thể có tính dị hướng, còn chất rắn đa tinh thể có tính đẳng hướng.
+ Chất rắn vô định hình không có cấu trúc tinh thể, do đó không có dạng hình học xác định, không có nhiệt độ nóng chảy (hoặc đông đặc) xác định và có tính đẳng hướng.
Lời giải chi tiết:
Các chất rắn được phân thành hai loại: kết tinh và vô định hình.
Câu hỏi 40 :
Đặc điểm và tính chất nào dưới đây liên quan đến chất rắn vô định hình?
- A có nhiệt độ nóng chảy không xác định
- B có dạng hình học xác định
- C có cấu trúc tinh thể
- D có tính dị hướng.
Đáp án: A
Phương pháp giải:
+ Các chất rắn được phân thành hai loại: kết tinh và vô định hình.
+ Chất rắn kết tinh có cấu trúc tinh thể, do đó có dạng hình học và nhiệt độ nóng chảy xác định.
+ Chất rắn kết tinh có thể là chất đơn tinh thể hoặc chất đa tinh thể. Chất rắn đơn tinh thể có tính dị hướng, còn chất rắn đa tinh thể có tính đẳng hướng.
+ Chất rắn vô định hình không có cấu trúc tinh thể, do đó không có dạng hình học xác định, không có nhiệt độ nóng chảy (hoặc đông đặc) xác định và có tính đẳng hướng.
Lời giải chi tiết:
Chất rắn vô định hình không có cấu trúc tinh thể, do đó không có dạng hình học xác định, không có nhiệt độ nóng chảy (hoặc đông đặc) xác định và có tính đẳng hướng.
\( \Rightarrow \) Đặc điểm, tính chất liên quan đến chất rắn vô định hình là: có nhiệt độ nóng chảy không xác định.
