Đề bài
(mỗi câu 1 điểm)
Câu 1: Trong dao động điều hòa
A.lực tác dụng lên vật trái dấu với li độ và có độ lớn tỉ lệ với độ lớn của li độ.
B.vận tốc luôn trễ pha \(\dfrac{\pi }{2}\) so với li độ.
C.gia tốc luôn trễ pha \(\dfrac{\pi }{2}\) so với vận tốc.
D.gia tốc và li độ luôn cùng pha.
Câu 2: Một vật dao động điều hòa theo phương trình: \(x = 3cos\left( {2\ t + \dfrac{\pi }{2}} \right)\,(cm)\)
Tần số của dao động là:
\(\begin{array}{l}A.\dfrac{\pi }{2}Hz\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B.2\pi \,Hz\\C.\dfrac{{1}}{\pi}\,Hz\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,D.3\,Hz\end{array}\)
Câu 3: Một vật nhỏ khối lượng m = 0,01kg treo ở đầu một lò xo có độ cứng k = 4 N/m, dao động điều hòa quanh vị trí cân bằng. Chu kì dao động của vật là:
A.0,624s B.0,314s
C.0,196s D.0,157s
Câu 4: Một chất điểm dao động điều hòa trên đoạn thẳng dài 8cm, tần số Hz. Lúc t = 0, chất điểm ở vị trí cân bằng và bắt đầu đi theo chiều dương. Phương trình dao động của chất điểm là:
\(\begin{array}{l}A.x = 4cos\left( {10\pi t - \dfrac{\pi }{2}} \right)\,(cm)\\B.x = 4cos(10\pi t + \pi )\,(cm)\\C.x = 4\sin \left( {10\pi t - \dfrac{\pi }{2}} \right)\,(cm)\\D.x = 4\sqrt 2 \sin (10\pi t + \pi )\,(cm)\end{array}\)
Câu 5: Một con lắc lò xo gồm một quả cầu nhỏ gắn vào đầu một lò xo, dao động điều hòa với biên độ 2,5 cm dọc theo trục Ox, với chu kì 1,2s. Vào thời điểm t = 0, quả cầu đi qua vị trí cân bằng theo chiều dương của trục Ox. Hỏi vào thời điểm nào sau đây quả cầu có li độ x = 1,25 cm?
A.t = 0,04s B.t = 0,75s
C.t = 0,5s D.t = 0,6s
Câu 6: Một vật dao động điều hòa theo phương trình \(x = 2cos\left( {\pi t - \dfrac{{3\pi }}{4}} \right)\) trong đó x tính bằng cm, t tính bằng giây (s). Vào thời điểm t =3,5s vật đi qua vị trí có li độ
\(\begin{array}{l}A.x = 2cm\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,B.x = 2cm\\C.\sqrt 2 \,cm\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,D. - \sqrt 2 cm\end{array}\)
Câu 7: Một vật nặng treo vào đầu lò xo làm cho lò xo dãn ra 4 cm. Đầu kia treo vào một điểm O cố định. Hệ dao động điều hòa theo phương thẳng đứng. Cho \(g = {\pi ^2}\,m/{s^2}.\) Chu kì dao động của hệ là:
A.0,8s B.0,4s
C.0,2s D.1,6s
Câu 8: Một con lắc lò xo gồm lò xo có độ cứng k = 100 N/m và vật nặng có khối lượng m, dao động điều hòa theo trục Ox nằm ngang. Thế năng của con lắc đó khi vật đi qua vị trí có li độ x = 3cm theo chiều âm là:
A.0,045J B.0,09J
C.-0,045J D.-0,09J
Câu 9: Một đầu của lò xo được treo vào điểm cố định O, đầu kia treo một quả nặng m1 thì chu kì T1 = 0,6s. Khi thay đổi quả nặng m2 vào thì chu kì dao động bằng T2 = 0,8s. Chu kì dao động khi treo đồng thời m1 và m2 vào lò xo là:
A.T = 1,6s B.T = 1,4s
C.T = 1,0s D. T = 1,2s
Câu 10: Một con lắc lò xo dao động điều hòa với biên độ A = 10,0cm và cơ năng 0,8J. Độ cứng của lò xo là:
A.80 N/m B.40 N/m
C.1,6 N/m D.160 N/m
Lời giải chi tiết
Đáp án
|
1. A |
2. C |
3. B |
4. A |
5. C |
|
6. D |
7. B |
8. A |
9. C |
10. D |
Giải chi tiết
Câu 1:
Phương pháp
Sử dụng lý thuyết về dao động điều hòa:
+ Phương trình li độ, vân tốc, gia tốc.
+ Biểu thức của lực trong dao động điều hòa.
Cách giải
A đúng
B sai vì vận tốc sớm pha hơn li độ góc \(\dfrac{\pi }{2}\)
C sai vì gia tốc sớm pha hơn vận tốc góc \(\dfrac{\pi }{2}\)
D sai vì gia tốc và li độ luôn ngược pha.
Chọn A
Câu 2:
Phương pháp
Sử dụng phương trình li độ \(x = A\cos \left( {\omega t + \varphi } \right)\)
Sử dụng công thức \(f = \frac{\omega }{{2\pi }}\)
Cách giải
Từ phương trình suy ra tốc độ góc \(\omega = 2{\rm{r}}a{\rm{d}}/s\)
Suy ra tần số của dao động là: \(f = \frac{\omega }{{2\pi }} = \frac{2}{{2\pi }} = \frac{1}{\pi }\left( {Hz} \right)\)
Chọn C
Câu 3:
Phương pháp
Sử dụng biểu thức \(T = 2\pi \sqrt {\frac{m}{k}} \)
Cách giải
\(T = 2\pi \sqrt {\dfrac{m}{k}} = 2\pi \sqrt {\dfrac{{0,01}}{4}} = 0,314s\)
Chọn B
Câu 4:
Phương pháp
Sử dụng cách lý thuyết viết phương trình dao động của chất điểm.
Cách giải
Biên độ dao động của chất điểm là: \(A = \dfrac{8}{2} = 4cm\)
Tần số góc \(\omega = 2\pi f = 10\pi \,rad/s\)
Khi t = 0, x = 0 và v > 0.
Do đó ta có: \(cos\varphi = 0,\sin \varphi < 0.\)
Vậy \(\varphi = - \dfrac{\pi }{2}\)
Phương trình dao động của chất điểm là: \(x = 4cos\left( {10\pi t - \dfrac{\pi }{2}} \right)\,(cm)\)
Chọn A
Câu 5:
Phương pháp
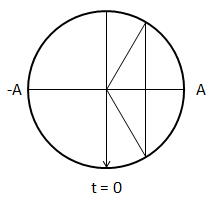
Sử dụng vòng tròn lượng giác.
Cách giải
Ta có: A = 2,5 cm, T = 1,2 s
Thời điểm t = 0 quả cầu đi qua vị trí cân bằng theo chiều dương.
Sử dụng vòng tròn lượng giác:
Suy ra thời điểm quả cầu có li độ x = 1,25 cm = A/2 là:
\(\left[ \begin{array}{l}\varphi = \frac{\pi }{6} \Rightarrow t = \frac{T}{{12}} = \frac{{1,2}}{{12}} = 0,1s\\\varphi = \frac{{5\pi }}{6} \Rightarrow t = \frac{{5T}}{{12}} = \frac{{5.1,2}}{{12}} = 0,5s\end{array} \right.\)
Chọn C
Câu 6:
Phương pháp
Cách giải
\(t = 3,5{\rm{s}} \Rightarrow x = 2\cos \left( {\pi .3,5 - \frac{{3\pi }}{4}} \right) \\= - \sqrt 2 cm\)
Chọn D
Câu 7:
Phương pháp
Sử dụng công thức \(T = 2\pi \sqrt {\frac{{\Delta l}}{g}} \)
Cách giải
Ta có: \(T = 2\pi \sqrt {\frac{{\Delta l}}{g}} = 2\pi \sqrt {\frac{{0,04}}{{10}}} = 0,4{\rm{s}}\)
Chọn B
Câu 8:
Phương pháp
Sử dụng công thức: \({{\rm{W}}_t} = \frac{1}{2}k{{\rm{x}}^2}\)
Cách giải
\({{\rm{W}}_t} = \dfrac{1}{2}k.{x^2} = \dfrac{1}{2}.100.0,{03^2} = 0,045J\)
Chọn A
Câu 9:
Chu kì kì dao động của hệ lò xo và vật nặng m1 là: \({T_1} = 2\pi \sqrt {\dfrac{{{m_1}}}{k}} \)
Chu kì dao động của hệ lò xo và vật nặng m2 là: \({T_2} = 2\pi \sqrt {\dfrac{{{m_2}}}{k}} \)
Chu kì dao động của hệ lò xo và hai vật nặng (m1+m1) là
\({T_{12}} = 2\pi \sqrt {\dfrac{{{m_1} + {m_2}}}{k}} \)\(\, = \sqrt {\dfrac{{4{\pi ^2}.{m_1}}}{k} + \dfrac{{4{\pi ^2}.{m_2}}}{k}} \)\(\,= \sqrt {T{}_1^2 + T{}_2^2} = 1s\)
Chọn C
Câu 10:
\(k = \dfrac{{2{\rm{W}}}}{{{A^2}}} = 160N/m.\)
Chọn D
soanvan.me