Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Đề số 1 – Vật lý 11

Đề bài

PHẦN TRẮC NGHIỆM (6 điểm, mỗi câu 0,3 điểm)

Câu 1: Chọn câu sai. 

Công của lực điện trường làm di chuyển điện tích q từ điểm A đến điểm B trong điện trường đều E:

A. Tỉ lệ với độ lớn điện tích q di chuyển.

B. Chỉ phụ thuộc vào vị trí điểm A và điểm B. 

C. Bằng độ giảm của thế năng tĩnh điện của q giữa A và B.

D. Phụ thuộc vào hình dạng đường đi từ A đến B.

Câu 2: Hai quả cầu nhỏ có điện tích lần lượt là \({q_1}\, = \,{2.10^{ - 8}}\,C,{q_2}\, = \,4,{5.10^{ - 8}}\,C\) tác dụng với nhau một lực bằng 0,1 N trong chân không. Khoảng cách giữa chúng bằng:

A. 0,9 m.         B. 9 cm.

C. 9 mm.         D. 3 mm.

Câu 3: Hai điện tích điểm đặt trong chân không cách nhau 4 cm đẩy nhau một lực F = 10 N. Để lực đẩy giữa chúng là 2,5 N thì khoảng cách giữa chúng là:

A. 1 cm.          B. 4 cm.

C. 8 cm.           D. 10 cm.

Câu 4: Cho hai điện tích điểm nằm ở hai điểm A và B và có cùng độ lớn, cùng dấu. Cường độ điện trường tại một điểm trên đường trung trực của AB có phương

A. vuông góc với đường trung trực của AB.

B. trùng với đường trung trực của AB.

C. trùng với đường nối của AB.

D. tạo với đường nối của AB góc 45⁰.

Câu 5: Hiệu điện thế giữa hai điểm M, N là U_MN = 100 V. Chọn phát biểu đúng.

A. Điện thế ở M là 100 V.

B. Điện thế ở N bằng 0.

C. Điện thế ở M có giá trị dương, ở N có giá trị âm.

D. Điện thế ở M cao hơn điện thế ở N 100 V.

Câu 6: Độ lớn điện trường tại một điểm gây ra bởi một điện tích điểm không phụ thuộc vào

A. khoảng cách từ điểm đang xét đến điện tích đó.

B. độ lớn điện tích thử.

C. hằng số điện môi của môi trường.

D. độ lớn điện tích đó.

Câu 7: Đặt một điện tích thử có điện tích \(q\, = \, - 1\,\mu C\) tại một điểm, nó chịu một lực điện 1 mN có hướng từ trái sang phải. Cường độ điện trường có độ lớn và hướng là:

A. 1000 V/m, từ trái sang phải.

B. 1000 V/m, từ phải sang trái.

C. 1 V/m, từ trái sang phải.

D. 1 V/m, từ phải sang trái.

Câu 8: Phát biểu nào sau đây về tụ điện là không đúng?

A. Điện dung đặc trưng cho khả năng tích điện của tụ.

B. Điện dung của tụ càng lớn thì tích được điện lượng càng lớn.

C. Điện dung của tụ có đơn vị là fara (F).

D. Hiệu điện thế càng lớn thì điện dung của tụ càng lớn

Câu 9: Nhận xét nào sau đây là sai?

A. Cường độ điện trường của điện tích điểm tại vô cực bằng không.

B. Cường độ điện trường bên trong vật dẫn tích điện bằng không.

C. Điện thế trong điện trường của điện tích điểm tại vô cực bằng không.

D. Cường độ điện trường bên trong chất điện môi nhỏ hơn bên ngoài chất điện môi \(\varepsilon \) lần.

Câu 10: Công của lực điện làm dịch chuyển một điện tích điểm q từ điểm M đến điểm N trong điện trường, thì không phụ thuộc vào

A. vị trí của điểm M.

B. hình dạng của đường đi MN.

C. độ lớn của điện tích q.

D. độ lớn cường độ điện trường tại các điểm trên đường đi.

Câu 11: Một tụ điện phẳng không khí được tích điện rồi ngắt khỏi nguồn điện. Sau khi ngắt khỏi nguồn người ta nhúng tụ điện ngập vào dầu hỏa. So với khi chưa nhúng thì:

A. Hiệu điện thế tăng lên.

B. Cường độ điện trường trong tụ điện giảm \(\varepsilon \) lần.

C. Điện tích trên tụ giảm \(\varepsilon \) lần.

D. Hiệu điện thế giữa hau bản không đổi.

Câu 12: Phát biểu nào sau đây là sai?

A. Hiệu điện thế giữa hai điểm đặc trưng cho khả năng thực hiện công của điện trường giữa hai điểm đó.

B. Hiệu điện thế giữa hai điểm đo bằng thương số giữa công mà lực điện thực hiện khi làm dịch chuyển một điện tích q từ điểm nọ đến điểm kia và điện tích đó.

C. Giá trị của hiệu điện thế giữa hai điểm phụ thuộc vào mốc tính điện thế.

D. Hiệu điện thế giữa hai điểm trong điện trường là đại lượng vô hướng có thể dương hoặc âm.

Câu 13: Một êlectron bay từ điểm A đến điểm B trong điện trường có điện thế \({V_A} = 150\,V,\,{V_B} = \,50\,V.\) Độ biến thiên động năng của êlectron khi chuyển động từ A đến B là:

A. ∆W_đ = 3,2.10^-17 J.

B. ∆W_đ = -1,6.10^-17 J.

C. ∆W_đ = 1,6.10^-17 J.

D. ∆W_đ = -3,2.10^-17 J.

Câu 14: Hia quả cầu nhỏ giống hệt nhau được tích điện cùng dấu nhưng có giá trị khác nhau q₁ và q₂. Đặt hai quả cầu tại hai điểm A, B cách nhau 1 khoảng r trong chân không thì chúng đẩy nhau một lực F₁. Cho hai quả cầu tiếp xúc nhau rồi đặt lại vào vị trí A, B như cũ thấy chúng đẩy nhau một lực F₂. Nhận định nào sau đây đúng?

A. F₁ > F₂.                   B. F₁ < F₂.

C. F₁ = F₂.                   D. không xác định được.

Câu 15: Điện tích Q sinh ra xung quanh nó một điện trường. Đại lượng nào dưới đây không liên quan đến cường độ điện trường tại một điểm M của điện tích Q?

A. Điện tích Q.

B. Khoảng cách từ M đến Q.

C. Điện tích thử q.

D. Môi trường xung quanh.

Câu 16: Một tụ điện phẳng không khí được mắc vào hai cực của nguồn điện một chiều có suất điện động E không đổi. Sau khi tích điện, tụ được cắt khỏi nguồn điện rồi kéo cho khoảng cách giữa các bản tụ tăng lên gấp đôi. So với trước khi kéo xa hai bản cực, cường độ điện trường trong tụ điện

A. tăng 2 lần.              B. giảm 2 lần.

C. tăng 4 lần.               D. không thay đổi.

Câu 17: Hai tụ điện có điện dung \({C_1}\, = \,{C_2}\, = \,{C_0}\) được mắc song song, rồi mắc nối tiếp với tụ điện có điện dung \({C_3}\, = \,{C_0}\) thành bộ. Mắc bộ tụ điện và hai cực một nguồn điện một chiều có suất điện dộng E = 12 V. Hiệu điện thế trên hai đầu tụ điện C₁ bằng:

A. 8 V.                        B. 4 V.

C. 6 V.                        D. 3 V.

Câu 18: Hai tụ điện có điện và hiệu điện thế giới hạn lần lượt là \({C_1} = \,20\,pF,\,{U_1} = 200\,V;\,\)\({C_2} = 30\,pF,\,{U_2} = 400\,V\) được mắc nối tiếp thành bộ . Hiệu điện thế tối đa mà bộ tụ chịu đựng được là:

A. 600 V.        B. 300 V.

C. 333 V.        D. 400V.

Câu 19: Một điện tích điểm q = 10^-9 C chuyển động từ đỉnh A đến đỉnh B của một tam giá đều ABC. Tam giác đều ABC nằm trong một điện trường đều có cường độ điện trường E = 2.10⁴ V/m. Đường sức của điện trường này song song với cạnh BC và có chiều từ B đến C. Cạnh của tam giác bằng 20 cm. Công của lực điện trường khi q dịch chuyển từ đỉnh A đến B bằng:

A. 4.10^-6 J.                   B. -4.10^-6 J.

C. 2.10^-6 J.                   D. -2.10^-6 J.

Câu 20: Có hai điểm A và B cùng nằm trên một đường sức điện trường của điện tích điểm. Biết rằng cường độ điện trường tại A là E_A= 400 V/m, tại B là 100 V/m. Cường độ điện trường tại trung điểm của AB là:

A. 150,0 V/m.             B. 250,0 V/m.

C. 177,8 V/m.             D. 189,8 V/m.

PHẦN TỰ LUẬN (4 điểm)

Câu 21 (1 điểm): Chi hai điện tích \({q_1} = 2\,\mu C,\,{q_2} = 8\,\mu C\) đặt tại hai điểm A và B trong chân không AB = 30 cm. Xác định vị trí của điểm M để nếu đặt tại M một điện tích q₀ bất kì thì lục điện tổng hợp tác dụng lên q₀ bằng 0.

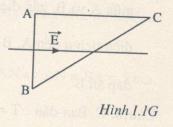
Câu 22 (3 điểm): Ba điểm A, B, C là ba đỉnh của một tam giác vuông trong điện trường đều, cường độ E = 1000 V/m. Đường sức điện trường song song với AC, chiều đường sức là chiều từ A đến C. Biết AC = 8 cm, AB = 6 cm.Góc BAC = 90⁰.

a) Tính hiệu điện thế giữa các điểm A và B; A và C; B và C.

b) Tính công của lực điện để dịch chuyển một êlectron từ điểm B tới điểm C.

c) Một êlectron chuyển động không vận tốc ban đầu, xuất phát tại A, xác định vận tốc của êlectron đó khi nó di chuyển tới điểm C của tam giác đã cho.

Lời giải chi tiết

PHẦN TRẮC NGHIỆM

1. D	2. C	3. C	4. B	5. D	6. B	7. B	8. D	9. C	10. B
11.B	12.C	13.B	14.B	15.C	16.D	17.B	18.C	19.D	20.C

Câu 1:

Phương pháp 

Sử dụng lý thuyết về công của lực điện trường.

Cách giải

Công của lực điện trường làm di chuyển điện tích q từ điểm A đến điểm B trong điện trường đề E không phụ thuộc vào hình dạng đường đi từ A đến B mà chỉ phụ thuộc vào vị trí điểm A và điểm B. => D sai

Chọn D

Câu 2:

Phương pháp

Sử dụng biểu thức định luật Cu-lông:

\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Cách giải

Ta có:

\(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} \Leftrightarrow 0,1 = {9.10^9}.\frac{{{{2.10}^{ - 8}}.4,{{5.10}^{ - 8}}}}{{{r^2}}}\\ \Leftrightarrow r = {9.10^{ - 3}}m = 9mm\)

Chọn C

Câu 3:

Phương pháp

Sử dụng biểu thức định luật Cu-lông: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Cách giải

Ta có:

\(\left\{ \begin{array}{l}{F_1} = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r_1}^2}} = 10\\{F_2} = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r_2}^2}} = 2,5\end{array} \right. \Rightarrow \frac{{{F_1}}}{{{F_2}}} = \frac{{r_2^2}}{{r_1^2}} = 4\\ \Leftrightarrow {r_2} = 2{{\rm{r}}_1} = 2.4 = 8cm\)

Chọn C

Câu 4:

Phương pháp

\(\overrightarrow E \) hướng ra xa điện tích nếu q > 0

\(\overrightarrow E \) hướng vào trong điện tích nếu q < 0

Tổng hợp lực theo quy tắc hình bình hành

Cách giải

Giả sử hai điện tích cùng dấu âm, ta biểu diễn các vecto cường độ điện trường như hình vẽ.

 

Chọn B

Câu 5:

Phương pháp

Sử dụng lý thuyết điện thế, hiệu điện thế.

Cách giải

\({U_{MN}} = {V_M} - {V_N}\)

Trong điện trường, vecto cường độ điện trường có hướng từ nơi có điện thế cao sang nơi có điện thế thấp.

Chọn D

Câu 6:

Phương pháp

Sử dụng công thức: \(E = k\frac{{\left| q \right|}}{{\varepsilon {r^2}}}\)

Cách giải

Ta có: \(E = k\frac{{\left| q \right|}}{{\varepsilon {r^2}}}\)

=> E không phụ thuộc vào độ lớn điện tích thử.

Chọn B

Câu 7:

Phương pháp

Cách giải

Do điện thích thử q < 0 nên \(\overrightarrow E  \uparrow  \downarrow \overrightarrow F \) => \(\overrightarrow E \) có hướng từ phải sang trái và có độ lớn:

\(E = \frac{F}{{\left| q \right|}} = \frac{{{{10}^{ - 3}}}}{{{{10}^{ - 6}}}} = 1000V/m\)

Chọn B

Câu 8:

Phương pháp

Sử dụng lý thuyết định nghĩa điện dung của tụ điện.

Sử dụng công thức: \(C = \frac{Q}{U}\)

Cách giải

- Điện dung của tụ điện đặc trưng cho khả năng tích điện của tụ, có đơn vị là Fa-ra => A,C đúng.

- Ta có: \(C = \frac{Q}{U}\) => điện dung C tỉ lệ thuận với điện tích Q và tỉ lệ nghịch với hiệu điện thế U.

=> B đúng, D sai

Chọn D

Câu 9:

Chọn C

Câu 10:

Phương pháp

Sử dụng lý thuyết về công của lực điện trường.

Cách giải

Công của lực điện trường làm di chuyển điện tích q từ điểm M đến điểm N trong điện trường đề E không phụ thuộc vào hình dạng đường đi từ M đến N mà chỉ phụ thuộc vào vị trí điểm M và điểm N.

Chọn B

Câu 11:

Phương pháp

Sử dụng công thức tính điện dung tụ phẳng: \(C = \frac{{\varepsilon S}}{{4\pi k{\rm{d}}}}\)

Cách giải

Tụ được tách khỏi nguồn và nhúng vào điện môi nên không có sự thay đổi điện tích giữa các bản tụ.

Ban đầu tụ đặt trong không khí thì \(C = \frac{S}{{4\pi k{\rm{d}}}}\)

Sau khi nhúng vào điện môi thì \(C = \frac{{\varepsilon S}}{{4\pi k{\rm{d}}}}\)

=> C tăng.

Lại có: \(U = \frac{Q}{C}\) nên C tăng thì U giảm , U = E.d => E giảm

Vậy điện tích của tụ không thay đổi và hiệu điện thế giữa hai bản giảm, cường độ điện trường E giảm.

Chọn B

Câu 12:

Phương pháp

Sử dụng lý thuyết hiệu điện thế.

Cách giải

Ta có: \({U_{MN}} = {V_M} - {V_N}\) không phụ thuộc vào việc chọn mốc tính điện thế, việc chọn mốc chỉ ảnh hưởng đến giá trị V.

Chọn C 

Câu 13: B. Độ biến thiên động năng bằng công của lực tĩnh điện

∆W_đ = A = qU_MN; U_MN = V_A – V_B, thay số ta được đáp án B.

Câu 14: B.

Câu 15: C.

Câu 16: D. Dựa vào biểu thức cường độ điện trường và điện dung của tụ điện phẳng: \(E\, = \,\dfrac{U}{d}\, = \,\dfrac{q}{{dC}},\,C\, = \,\dfrac{S}{{{{9.10}^9}.4\pi d}},\) ta thu được đáp án D.

Câu 17: B. Ta có \(C\, = \,\dfrac{{({C_1}\, + \,{C_2}){C_3}}}{{{C_1}\, + \,{C_2}\, + \,{C_3}}};\,{q_1}\, + \,{q_2}\, = \,q\)

\(\Rightarrow 2\,{U_1}\, = \,EC,\) thay số được đáp án B.

Câu 18: C.

Câu 19: D. Lực điện là laoij lực thế nên công của lực không phụ thuộc vào hình dạng đường đi, ta có \(d\, = \,AB\cos {60^0};\,A\, = \,qU\, = \,qdE,\) thay số được đáp án D.

Câu 20: C. Từ biểu thức tính cường độ điện trường \(E\, = \,\dfrac{{k\left| q \right|}}{{{r^2}}},\) với \({r_M}\, = \,\dfrac{{{r_A}\, + \,{r_B}}}{2},\) giải ra ta được đáp án C.

PHẦN TỰ LUẬN

Câu 21:

q₁ và q₂ cùng dấu nên để lực điện tác dụng lên q₀ bằng không thì điểm đó phải nằm trên đoạn nối giữa q₁ và q₂ (Hình I.1G)

\(\overrightarrow {{F_1}} \, = \, - \overrightarrow {{F_2}} ,\) độ lớn \({F_1}\, = \,{F_2}\left\{ \begin{array}{l}\dfrac{{{q_1}}}{{r_1^2}} = \dfrac{{{q_2}}}{{r_2^2}}\\{r_1}\, + \,{r_2}\, = \,30\,cm\end{array} \right.\\ \Rightarrow {r_1}\, = \,10\,cm,\,{r_2}\, = \,20\,cm.\)

 

Câu 22:

a) Hiệu điện thế:

- Vì điểm A và B nằm trên cùng một mặt phẳng thế nên điện thế giữa hai điểm đó là như nhau, do đó: U_AB = 0.

- Ta có U_AC = E.AC = 1000.0,08 = 80 V.

- Tương tự:

\({U_{BC}}\, = \,E.AC\, = \,1000.0,08\, = \,80\,V.\)

b) Lực điện trường là loại lực thế nên công của chúng không phụ thuộc vào đường đi, do đó:

\(A\, = \,\left| e \right|{U_{BC}}\, = \,\left| e \right|{U_{AC}}\, \)\(= \,1,{6.10^{ - 19}}.80\, = \,12,{8.10^{ - 18}}\,J.\)

c) Công của lực điện trường bằng độ biến thiên động năng của êlectron:

\({A_{AC}}\, = \,\dfrac{{mv_C^2}}{2} - \dfrac{{mv_0^2}}{2}\)

\(\Rightarrow {v_C} = \sqrt {\dfrac{{2{A_{AC}}}}{m}}  = \sqrt {\dfrac{{{{2.128.10}^{ - 19}}}}{{9,{{1.10}^{ - 31}}}}}\)\(\,  \approx 5,{3.10^6}\,m/s.\)

soanvan.me