Đề bài
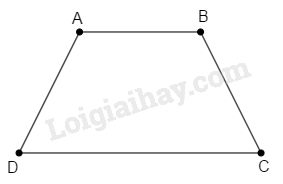
Câu 1: Cho hình thang \(ABCD (AB//CD).\) Các khẳng định sau đúng hay sai?
a) Nếu \(\widehat{A}+\widehat{D}={{180}^{o}}\) thì \(ABCD\) là hình thang cân.
b) Nếu \(\widehat{B}+\widehat{D}={{180}^{o}}\) thì \(ABCD\) là hình thang cân.
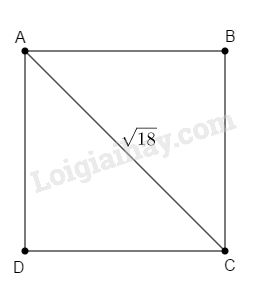
Câu 2: Hình vuông có đường chéo bằng \(\sqrt {18} \) thì cạnh bằng
(A) \(2\) (B) \(3\)
(C) \(6\) (D) \(\sqrt 3 \)
Hãy chọn câu trả lời đúng.
Câu 3: Xét các tam giác vuông \(ABC\) có cạnh huyền \(BC\) cố định, \(BC = 4 cm\), \(I\) là trung điểm của \(BC\). Tập hợp các điểm \(A\) là
(A) Đường tròn \((B;2cm)\)
(B) Đường tròn \((C;2cm)\)
(C) Đường tròn \((I;2cm)\)
(D) Đường tròn \((I;4cm)\)
Hãy chọn câu trả lời đúng.
Câu 4: Cho tam giác \(ABC\) vuông tại \(A, M\) là trung điểm của \(BC.\) Gọi \(I\) là điểm đối xứng với \(M\) qua \(AB,\) gọi \(D\) là giao điểm của \(MI\) và \(AB.\) Gọi \(K\) là điểm đối xứng với \(M\) qua \(AC,\) gọi \(E\) là giao điểm của \(MK\) và \(AC.\)
a) Tứ giác \(ADME\) là hình gì? Vì sao?
b) Tứ giác \(AMCK\) là hình gì? Vì sao?
c) Chứng minh hai điểm \(I\) và \(K\) đối xứng với nhau qua điểm \(A.\)
d) Nếu tam giác \(ABC\) vuông cân tại \(A\) thì các tứ giác \(ADME, AMCK\) là hình gì? Vì sao? Vẽ hình tương ứng.
Lời giải chi tiết
Câu 1:
Phương pháp:
Sử dụng:
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc trong cùng phía bù nhau.
- Hình thang có hai góc kề với một đáy bằng nhau là hình thang cân.
Lời giải:
Vì \(AB//CD\) nên \(\widehat{A}+\widehat{D}={{180}^{o}}\) (1) (hai góc trong cùng phía).
\(\widehat{B}+\widehat{D}={{180}^{o}}\) (2)
Từ (1) và (2) suy ra \(\widehat{A}=\widehat{B}\) nên ABCD là hình thang cân.
Do đó a) sai; b) đúng.
Câu 2:
Phương pháp:
Sử dụng:
- Hình vuông là tứ giác có bốn cạnh bằng nhau, bốn góc bằng nhau.
- Định lí Pytago: Bình phương của cạnh huyền bằng bình phương của hai cạnh góc vuông.
Lời giải:
Gọi cạnh hình vuông là \(a\) \((a>0)\).
Áp dụng định lí Pytago vào \(\Delta ADC\) vuông tại \(D\) ta có:
\(\begin{align}& A{{D}^{2}}+D{{C}^{2}}=A{{C}^{2}} \\& {{a}^{2}}+{{a}^{2}}={{\left( \sqrt{18} \right)}^{2}} \\& 2{{a}^{2}}=18 \\& \Rightarrow {{a}^{2}}=18:2=9 \\ & \Rightarrow a=\sqrt{9}=3 \\\end{align}\)
Chọn B.
Câu 3:

Phương pháp:
Sử dụng: Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
Lời giải:
\(AI\) là đường trung tuyến ứng với cạnh huyền \(BC\) nên \(AI=BC:2=4:2=2cm\)
\(I\) là trung điểm của \(BC\), mà \(BC\) cố định nên \(I\) cố định. Do đó tập hợp các điểm \(A\) là đường tròn \((I;2cm)\).
Chọn C.
Câu 4:
Phương pháp:
- Tứ giác có ba góc vuông là hình chữ nhật.
- Tứ giác có hai đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường là hình thoi.
- Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy.
Lời giải:
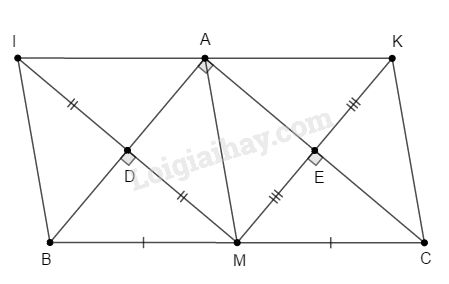
a) \(I\) đối xứng \(M\) qua \(AB\) nên \(AB\) là trung trực của \(MI.\) Do đó \(\widehat {ADM} = {90^o}\)
\(K\) đối xứng \(M\) qua \(AC\) nên \(AC\) là trung trực của \(MK.\) Do đó \(\widehat {AEM} = {90^o}\)
Tứ giác \(ADME\) có \(\widehat {ADM} = \widehat {AEM} = \widehat {DAE} = {90^o}\) nên là hình chữ nhật( Tứ giác có 3 góc vuông).
b) \(AM\) là trung tuyến ứng với cạnh huyền \(BC\) của \(\Delta ABC\) nên \(AM=MC\)
Xét hai tam giác vuông \(AME\) và \(CME\) có:
\(AM=MC\) (chứng minh trên)
\(ME\) chung
\(\widehat{AEM}=\widehat{CEM}={{90}^{o}}\)
\( \Rightarrow \Delta AME = \Delta CME\) (cạnh huyền – cạnh góc vuông).
\(\Rightarrow AE=CE\) (hai cạnh tương ứng).
Tứ giác \(AMCK\) có hai đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường nên là hình thoi.
c) \(AMCK\) là hình thoi nên \(AK=MC; AK//BC\) (1)
Chứng minh tương tự ta được: \(AMBI\) là hình thoi
Suy ra \(AI=BM; AI//BM\) (2)
Từ (1) và (2) suy ra \(AK=AI.\)
Qua \(A\) có hai đường thẳng cùng song song với \(BC\) nên theo tiên đề Ơclit \(I, A,K\) thẳng hàng.
Do đó \(I\) và \(K\) đối xứng với nhau qua điểm \(A.\)
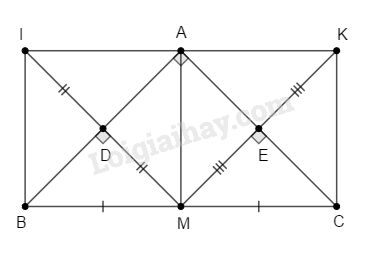
d) Tam giác \(ABC\) vuông cân tại \(A\) thì \(AD=AE\) nên \(ADME\) là hình vuông( Hình chữ nhật có 2 cạnh kề bằng nhau);
\(AE = ME \Rightarrow AC = MK\) do đó \(AMCK\) là hình vuông ( Hình thoi có 2 đường chéo bằng nhau).
Hình vẽ tương ứng:
soanvan.me
