Đề bài
Câu 1. (3 điểm) Hãy chọn kết quả đúng. Tam giác \(ABC\) có đường phân giác \(AD\left( {D \in BC} \right)\). Cho biết độ dài \(AB = 4,5cm,BD = 2,5cm,\) \(CD = 4cm\). (h.59)
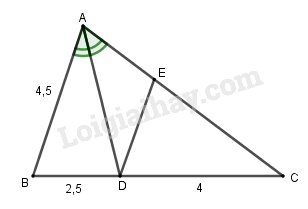
a) Độ dài của cạnh \(AC\) là:
A. \(7,5\)
B. \(7,2\)
C. \(11,7\)
D. \(2,8\)
b) Từ \(D\) kẻ \(DE//AB\left( {E \in AC} \right)\). Độ dài của đoạn thẳng \(DE\) là:
A. \(\dfrac{{36}}{{13}}\)
B. \(\dfrac{{36}}{5}\)
C. \(\dfrac{{36}}{{15}}\)
D. \(\dfrac{9}{5}\)
c) Độ dài của đoạn thẳng \(AE\) là:
A. \(\dfrac{{36}}{5}\)
B. \(\dfrac{{36}}{{13}}\)
C. \(\dfrac{{36}}{{25}}\)
D. \(\dfrac{{36}}{{15}}\)
Câu 2. (7 điểm) Tứ giác \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\), \(\widehat {ABD} = \widehat {ACD}\). Gọi \(E\) là giao điểm của hai đường thẳng \(AD\) và \(BC\) (h.60).
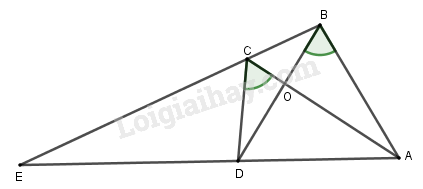
Chứng minh rằng:
a) \(\Delta AOB \backsim \Delta DOC\)
b) \(\Delta AOD \backsim \Delta BOC\)
c) \(EA.ED = EB.EC\)
Lời giải chi tiết
Câu 1:
Phương pháp:
a) Sử dụng tính chất đường phân giác của tam giác.
b) Sử dụng hệ quả của định lí Ta – let.
c) Sử dụng hệ quả của định lí Ta – let và các kết quả tính được ở trên.
Cách giải:
a) \(AD\) là phân giác của \(\widehat A\) nên \(\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}}\left( {tc} \right)\) \( \Rightarrow AC = \dfrac{{DC.AB}}{{BD}}\)\( = \dfrac{{4.4,5}}{{2,5}} = \dfrac{{36}}{5} = 7,2\).
Chọn B.
b) \(DE//AB\) nên theo hệ quả của định lý Ta – let ta có:
\(\dfrac{{DE}}{{AB}} = \dfrac{{DC}}{{BC}}\) \( \Rightarrow DE = \dfrac{{AB.DC}}{{BC}} = \dfrac{{4,5.4}}{{4 + 2,5}} = \dfrac{{36}}{{13}}\).
Chọn A.
c) \(ED//AB\) nên theo hệ quả của định lý Ta – let ta có:
\(\dfrac{{AE}}{{AC}} = \dfrac{{BD}}{{BC}}\) \( \Rightarrow AE = \dfrac{{AC.BD}}{{BC}}\) \( = \dfrac{{7,2.2,5}}{{2,5 + 4}} = \dfrac{{36}}{{13}}\)
Chọn B.
Câu 2:
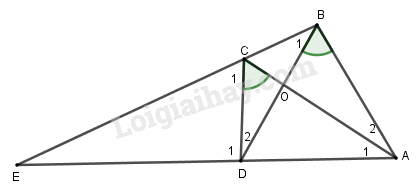
Phương pháp:
a) Sử dụng trường hợp đồng dạng góc – góc.
b) Sử dụng trường hợp đồng dạng cạnh – góc – cạnh.
c) Chứng minh hai tam giác \(ECD\) đồng dạng tam giác \(EAB\) và kết luận.
Cách giải:
a) Xét \(\Delta AOB\) và \(\Delta DOC\) có:
\(\widehat {ABO} = \widehat {DCO}\left( {gt} \right)\)
\(\widehat {AOB} = \widehat {DOC}\) (đối đỉnh)
\( \Rightarrow \Delta AOB \backsim \Delta DOC\) (đpcm).
b) Từ câu a, \(\Delta AOB \backsim \Delta DOC\)\( \Rightarrow \dfrac{{OA}}{{OD}} = \dfrac{{OB}}{{OC}}\left( {c.t.u} \right)\)
xét \(\Delta AOD\) và \(\Delta BOC\) có:
\(\widehat {AOD} = \widehat {BOC}\) (đối đỉnh)
\(\dfrac{{OA}}{{OD}} = \dfrac{{OB}}{{OC}}\left( {cmt} \right)\)
\( \Rightarrow \Delta AOD \backsim \Delta BOC\) (đpcm).
c) Ta có:
\(\widehat {{C_1}}\) là góc ngoài của tam giác \(BCD\) nên \(\widehat {{C_1}} = \widehat {{B_1}} + \widehat {{D_2}}\) (tính chất) (1)
Theo câu a) \(\Delta AOB \backsim \Delta DOC \Rightarrow \widehat {{A_2}} = \widehat {{D_2}}\) (góc tương ứng) (2)
Theo câu b) \(\Delta AOD \backsim \Delta BOC \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\) (góc tương ứng) (3)
Từ (1), (2) và (3) suy ra \(\widehat {{C_1}} = \widehat {{A_1}} + \widehat {{A_2}} = \widehat {BAE}\)
Xét tam giác \(ECD\) và tam giác \(EAB\) có:
\(\widehat E\) chung
\(\widehat {ECD} = \widehat {EAB}\left( {cmt} \right)\)
\( \Rightarrow \Delta ECD \backsim \Delta EAB\left( {g.g} \right)\)
\( \Rightarrow \dfrac{{EC}}{{EA}} = \dfrac{{ED}}{{EB}}\left( {c.t.u} \right)\) \( \Rightarrow EC.EB = EA.ED\left( {dpcm} \right)\).
soanvan.me
