Câu hỏi 1 :
Phương trình dao động của điện tích trong mạch dao động LC là \(q = {Q_0}\cos (\omega t + \varphi )\). Biểu thức của dòng điện trong mạch là:
- A
\(i = \omega {Q_0}\cos (\omega t + \varphi )\)
- B
\(i = \omega {Q_0}\cos (\omega t + \varphi + \frac{\pi }{2})\)
- C
\(i = \omega {Q_0}\cos (\omega t + \varphi - \frac{\pi }{2})\)
- D
\(i = \omega {Q_0}\sin (\omega t + \varphi )\)
Đáp án: B
Phương pháp giải:
Xem lí thuyết mục 1
Lời giải chi tiết:
\(q = {Q_0}\cos (\omega t + \varphi )\)
Biểu thức của cường độ dòng điện trong mạch: \(i = q' = \omega {Q_0}\cos (\omega t + \varphi + \frac{\pi }{2})\)
Câu hỏi 2 :
Chiếu xiên từ không khí vào nước một chùm sáng song song rất hẹp (coi như một tia sáng) gồm ba thành phần đơn sắc: đỏ, lam và tím. Gọi rđ, \({r_\ell }\), rt lần lượt là góc khúc xạ ứng với tia màu đỏ, tia màu lam và tia màu tím. Hệ thức đúng là
- A
\({r_\ell } = {r_t} = {\rm{ }}{r_d}\)
- B
\({r_t} < {r_\ell } < {\rm{ }}{r_d}\)
- C
\({r_d} < {r_\ell } < {\rm{ }}{r_t}\)
- D
\({r_t} < {r_d} < {r_\ell }\)
Đáp án: B
Phương pháp giải:
Xem lí thuyết phần 1
Lời giải chi tiết:
Ta có:
Câu hỏi 3 :
Trong thí nghiệm Y-âng, vân tối thứ hai xuất hiện ở trên màn tại các vị trí cách vân sáng trung tâm là:
- A
\(\dfrac{{3i}}{2}\)
- B
\(\dfrac{i}{2}\)
- C
\(i\)
- D
\(2i\)
Đáp án: A
Phương pháp giải:
Áp dụng biểu thức xác định vị trí vân tối trên màn: \({x_t} = \left( {k + \dfrac{1}{2}} \right)i\)
Lời giải chi tiết:
Ta có vị trí vân tối trên màn: \({x_t} = \left( {k + \dfrac{1}{2}} \right)i\)
Vân tối thứ hai (ứng với \(k = 1\)) xuất hiện trên màn cách vân sáng trung tâm là \(\left( {1 + \dfrac{1}{2}} \right)i = \dfrac{{3i}}{2}\)
Câu hỏi 4 :
Một vật có khối lượng nghỉ \(5kg\) chuyển động với tốc độ \(v = 0,6c\) ( với \(c = 3.10^8m/s\) là tốc độ ánh sáng trong chân không). Theo thuyết tương đối, động năng của vật bằng:
- A \(1,{125.10^{17}}J\)
- B \(12,{7.10^{17}}J\)
- C \({9.10^{16}}J\)
- D \(2,{25.10^{17}}J\)
Đáp án: A
Phương pháp giải:
Áp dụng công thức anhxtanh \(m = \dfrac{{{m_0}}}{{\sqrt {1 - \dfrac{{{v^2}}}{{{c^2}}}} }}\)
Lời giải chi tiết:
Khối lượng tương đối tính của vật là \(m = \dfrac{{{m_0}}}{{\sqrt {1 - \dfrac{{{v^2}}}{{{c^2}}}} }} = \dfrac{5}{{\sqrt {1 - {{\left( {\dfrac{{0,6c}}{c}} \right)}^2}} }} = 6,25kg\)
Động năng của vật là \({W_d} = E - {E_0} = \left( {m - {m_0}} \right){c^2} = 1,25.{\left( {{{3.10}^8}} \right)^2} = 1,{125.10^{17}}J\)
Câu hỏi 5 :
Mạch chọn sóng gồm cuộn cảm có L biến thiên từ Lmin đến Lmax và tụ điện có điện dung C. Bước sóng nhỏ nhất mà mạch bắt được là:
- A
\({\lambda _{\min }} = c\frac{{\sqrt {{L_{{\rm{min}}}}C} }}{{2\pi }}\)
- B
\({\lambda _{\min }} = 2\pi c\sqrt {\frac{{{L_{{\rm{min}}}}}}{C}} \)
- C
\({\lambda _{\min }} = \frac{{2\pi c}}{{\sqrt {{L_{{\rm{max}}}}C} }}\)
- D
\({\lambda _{\min }} = 2\pi c\sqrt {{L_{{\rm{min}}}}C} \)
Đáp án: D
Phương pháp giải:
Xem lí thuyết phần 1
Lời giải chi tiết:
Bước sóng nhỏ nhất mà mạch bắt được: \({\lambda _{\min }} = 2\pi c\sqrt {{L_{{\rm{min}}}}C} \)
Câu hỏi 6 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng trắng, trên màn quan sát thu được hình ảnh giao thoa gồm:
- A
Chính giữa là vạch sáng trắng, hai bên có những dải màu.
- B
Một dải màu cầu vồng biến thiên liên tục từ đỏ đến tím.
- C
Các vạch sáng và tối xen kẽ cách đều nhau.
- D
Chính giữa là vạch sáng trắng, hai bên có những dải màu cách đều nhau.
Đáp án: A
Phương pháp giải:
Giao thoa Y–âng với nguồn sáng trắng
Ánh sáng trắng là tập hợp của vô số ánh sáng đơn sắc có màu biến thiên liên tục từ đỏ đến tím
Lời giải chi tiết:
Trong thí nghiệm giao thoa ánh sáng trắng của I – âng, trên màn quan sát thu được hình ảnh giao thoa gồm chính giữa là vạch sáng trắng, hai bên có những dải màu
Câu hỏi 7 :
Trong chân không, ánh sáng tím có bước sóng \(0,38\mu m\) . Mỗi phôtôn của ánh sáng này mang năng lượng xấp xỉ bằng:
- A
5,23. 10-20 J
- B
2,49.10-31 J
- C
5,23.10-19 J
- D
2,49.10-19 J
Đáp án: C
Phương pháp giải:
Năng lượng của photon ánh sáng:
\(\varepsilon {\text{ }} = {\text{ }}hf{\text{ }} = {\text{ }}hc/\lambda \)
Lời giải chi tiết:
Mỗi photon của ánh sáng tím mang năng lượng:
\(\varepsilon = \dfrac{{hc}}{\lambda } = \dfrac{{6,{{625.10}^{-34}}{{.3.10}^8}}}{{0,{{38.10}^{-6}}}} = 5,{23.10^{ - 19}}J\)
Câu hỏi 8 :
Chiếu một ánh sáng có bước sóng \(λ\) và năng lượng phôtôn là \(ɛ\) vào một chất huỳnh quang thì ánh sáng phát quang có bước sóng \(λ’\) và năng lượng phôtôn là \(ɛ’\). Biết
\(\dfrac{{\varepsilon '}}{\varepsilon } = 0,8\). Tỉ số \(\dfrac{{\lambda '}}{\lambda }\) bằng
- A
\(1,25\).
- B
\(0,8\).
- C
\(1\).
- D
\(1,5\)
Đáp án: A
Phương pháp giải:
Năng lượng phôtôn \(\varepsilon = \dfrac{{hc}}{\lambda }\)
Lời giải chi tiết:
Năng lượng phôtôn \(\varepsilon = \dfrac{{hc}}{\lambda }\): \(\varepsilon = \dfrac{{hc}}{\lambda } \to \dfrac{\varepsilon }{{\varepsilon '}} = \dfrac{{\dfrac{{hc}}{\lambda }}}{{\dfrac{{hc}}{{\lambda '}}}} = \dfrac{{\lambda '}}{\lambda } = \dfrac{1}{{0,8}} = 1,25\)
Câu hỏi 9 :
Mạch dao động điện từ điều hoà gồm cuộn cảm L và tụ điện C, khi tăng điện dung của tụ điện lên 4 lần thì tần số dao động của mạch
- A
Tăng lên 4 lần.
- B
Tăng lên 2 lần.
- C
Giảm đi 4 lần.
- D
Giảm đi 2 lần.
Đáp án: D
Phương pháp giải:
Vận dụng biểu thức xác định tần số dao động của mạch dao động điện từ LC: \(f = \dfrac{1}{{2\pi \sqrt {LC} }}\)
Lời giải chi tiết:
Ta có, tần số dao động của mạch LC dao động tự do: \(f = \dfrac{1}{{2\pi \sqrt {LC} }}\)
=> Khi tăng C lên 4 lần thì tần số dao động sẽ giảm đi 2 lần
Câu hỏi 10 :
Thông tin nào sau đây là sai khi nói về các định luật bảo toàn trong phản ứng hạt nhân?
- A
Tổng số hạt nuclon của hạt tương tác bằng tổng số nuclon của các hạt sản phẩm
- B
Tổng số các hạt proton của hạt tương tác bằng tổng các hạt proton của các hạt sản phẩm
- C
Tổng năng lượng toàn phần của các hạt tương tác bằng tổng năng lượng toàn phần của các hạt sản phẩm
- D
Tổng các vectơ động lượng của các hạt tương tác bằng tổng các vectơ động lượng của các hạt sản phẩm.
Đáp án: B
Phương pháp giải:
Xem lí thuyết phần 2
Lời giải chi tiết:
A, C, D - đúng
B - sai vì không có định luật bảo toàn số proton
Câu hỏi 11 :
Sóng điện từ dùng trong thông tin liên lạc trên mặt đất là
- A
Sóng ngắn
- B
Sóng dài
- C
Sóng trung
- D
Sóng cực ngắn
Đáp án: A
Lời giải chi tiết:
Sóng ngắn dùng trong thông tin liên lạc trên mặt đất vì:
+ Có năng lượng lớn
+ Bị phản xạ nhiêu lần giữa tầng điện li và mặt đất
Câu hỏi 12 :
Phát biểu nào sau đây là đúng khi nói về quang phổ?
- A
Quang phổ liên tục của nguồn sáng nào thì phụ thuộc thành phần cấu tạo của nguồn sáng ấy.
- B
Mỗi nguyên tố hóa học ở trạng thái khí hay hơi nóng sáng dưới áp suất thấp cho một quang phổ vạch riêng, đặc trưng cho nguyên tố đó.
- C
Để thu được quang phổ hấp thụ thì nhiệt độ của đám khí hay hơi hấp thụ phải cao hơn nhiệt độ của nguồn sáng phát ra quang phổ liên tục.
- D
Quang phổ hấp thụ là quang phổ của ánh sáng do một vật rắn phát ra khi vật đó được nung nóng.
Đáp án: B
Phương pháp giải:
Vận dụng lí thuyết về các loại quang phổ
Lời giải chi tiết:
A - sai vì quang phổ liên tục không phụ thuộc vào thành phần cấu tạo của nguồn sáng
B - đúng
C - sai vì để thu được quang phổ vạch hấp thụ thì nhiệt độ của đám khí hay hơi hấp thụ phải thấp hơn nhiệt độ của nguồn sáng phát ra quang phổ liên tục
D - sai vì quang phổ vạch hấp thụ là quang phổ của ánh sáng do khi chiếu ánh sáng trắng qua nguồn khí hay hơi có nhiệt độ thấp hơn của nguồn
Câu hỏi 13 :
Một mạch dao động điện từ LC gồm cuộn dây thuần cảm có độ tự cảm không đổi và tụ điện có điện dung thay đổi được. Điện trở của dây dẫn không đáng kể và trong mạch có dao động điện từ riêng. Khi điện dung có giá trị ${C_1}$ thì tần số dao động riêng của mạch là ${f_1}$. Khi điện dung có giá trị \({C_2} = {\rm{ }}4{C_1}\) thì tần số dao động điện từ riêng trong mạch là:
- A
${f_2} = {\rm{ }}0,25{f_1}$
- B
${f_2} = {\rm{ }}2{f_1}$
- C
${f_2} = {\rm{ }}0,5{f_1}$
- D
${f_2} = {\rm{ }}4{f_1}$
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính tần số dao động: \(f = \dfrac{1}{{2\pi \sqrt {LC} }}\)
Lời giải chi tiết:
Ta có: $\left\{ \begin{array}{l}{f_1} = \dfrac{1}{{2\pi \sqrt {L{C_1}} }}\\{f_2} = \dfrac{1}{{2\pi \sqrt {L{C_2}} }} = \dfrac{1}{{2\pi \sqrt {L.4{C_1}} }} = \dfrac{{{f_1}}}{2} = 0,5{f_1}\end{array} \right.$
Câu hỏi 14 :
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo. Cho biết bán kính Bo r0 = 5,3.10-11 m. Quỹ đạo dừng M của êlectron trong nguyên tử có bán kính
- A 47,7.10-10 m.
- B 4,77.10-10 m.
- C 1,59.10-11 m.
- D 15,9.10-11 m.
Đáp án: B
Phương pháp giải:
Sử dụng biểu thức tính bán kính: \(r_n=n^2r_0\)
Lời giải chi tiết:
Áp dụng tiên đề về trạng thái dừng của nguyên tử trong mẫu nguyên tử Bo
Quỹ đạo dừng M có \(n =3\)
\(\to r=n^2r_0=3^2.5,3.10^{-11}=4,77.10^{-10}m\)
Câu hỏi 15 :
Trong công nghiệp cơ khí, dựa vào tính chất nào sau đây của tia tử ngoại mà người ta sử dụng để tìm vết nứt trên bề mặt các vật kim loại:
- A
Kích thích nhiều phản ứng hóa học
- B
Kích thích phát quang nhiều chất
- C
Tác dụng lên phim ảnh
- D
Làm ion hóa không khí và nhiều chất khác
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết về tia tử ngoại
Lời giải chi tiết:
Trong công nghiệp cơ khí, dựa vào tính chất kích thích phát quang nhiều chất của tia tử ngoại mà người ta sử dụng để tìm vết nứt trên bề mặt các vật kim loại.
Câu hỏi 16 :
Đồng vị \({}_{92}^{234}U\) sau một chuỗi phóng xạ \(\alpha \) và \({\beta ^ - }\) biến đổi thành \({}_{82}^{206}Pb\). Số phóng xạ \(\alpha \) và \({\beta ^ - }\) trong chuỗi là
- A
7 phóng xạ \(\alpha \) , 4 phóng xạ \({\beta ^ - }\)
- B
5 phóng xạ \(\alpha \), 5 phóng xạ \({\beta ^ - }\)
- C
10 phóng xạ \(\alpha \), 8 phóng xạ \({\beta ^ - }\)
- D
16 phóng xạ \(\alpha \), 12 phóng xạ \({\beta ^ - }\)
Đáp án: A
Phương pháp giải:
Vận dụng lí thuyết về phóng xạ
+ Phóng xạ \(\alpha \;({}_2^4He)\)
+ Phóng xạ \({\beta ^ - }\;({}_{ - 1}^0e)\)
Lời giải chi tiết:
Ta có: \(\alpha \;({}_2^4He)\), \({\beta ^ - }\;({}_{ - 1}^0e)\)
Gọi số phóng xạ \(\alpha \) là a, số phóng xạ \({\beta ^ - }\) là b
Theo đề bài: \({}_{92}^{234}U\) biến đổi thành \({}_{82}^{206}Pb\)
Suy ra: \(\left\{ \begin{array}{l}4{\rm{a}} = 234 - 206\\2{\rm{a}} - b = 92 - 82\end{array} \right. \to \left\{ \begin{array}{l}a = 7\\b = 4\end{array} \right.\)
=> Số phóng xạ \(\alpha \) và \({\beta ^ - }\) trong chuỗi là 7 và 4
Câu hỏi 17 :
Theo mẫu nguyên tử Bo, trong nguyên tử hidro, bán kính quỹ đạo dừng K là r0. Khi electron chuyển từ quỹ đạo dừng O về quỹ đạo dừng M thì bán kính quỹ đạo giảm
- A
21r0
- B
24r0
- C
16r0
- D
2r0
Đáp án: C
Phương pháp giải:
Bán kính quỹ đạo dừng thứ n trong nguyên tử hidro là \(r = {{{r_0}}}{{{n^2}}}\)
Lời giải chi tiết:
Quỹ đạo O có n = 5; quỹ đạo M có n = 3
Bán kính quỹ đạo dừng M và O là:\({r_M} = {{{r_0}}}{{{3^2}}} = {{{r_0}}}{9};{r_O} = {{{r_0}}}{{{5^2}}} = {{{r_0}}}{{25}}\)
Vậy khi chuyển từ quỹ đạo O về M thì bán kính quỹ đạo giảm: 25r0 - 9r0 = 16r0
Câu hỏi 18 :
Hạt nhân nguyên tử chì có 82 prôtôn và 125 nơtrôn. Hạt nhân nguyên tử này có kí hiệu là:
- A
\({}_{82}^{125}Pb\).
- B
\({}_{82}^{207}Pb\).
- C
\({}_{125}^{82}Pb\).
- D
\({}_{207}^{82}Pb\).
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết về cấu tạo hạt nhân:
- Kí hiệu: \(_Z^AX\)
- Trong đó: A: số khối ( số Nuclon); Z: số Proton (p); N: số Notron (n); N = A – Z
Lời giải chi tiết:
Hạt nhân nguyên tử chì có 82 prôtôn và 125 nơtrôn \( \to Z = 82;N = 125 \to A = Z + N = 207 \to {}_{82}^{207}Pb\)
Câu hỏi 19 :
Phát biểu nào là sai?
- A
Điện trở của quang trở giảm mạnh khi có ánh sáng thích hợp chiếu vào.
- B
Nguyên tắc hoạt động của tất cả các tế bào quang điện đều dựa trên hiện tượng quang dẫn.
- C
Trong pin quang điện, quang năng biến đổi trực tiếp thành điện năng.
- D
Có một số tế bào quang điện hoạt động khi được kích thích bằng ánh sáng nhìn thấy.
Đáp án: B
Phương pháp giải:
Vận dụng lí thuyết về tính chất lượng tử của ánh sáng
Lời giải chi tiết:
A, C, D - đúng
B - sai vì : Các tế bào quang điện hoạt động dựa trên hiện tượng quang điện ngoài
Câu hỏi 20 :
Định nghĩa nào sau đây là về đơn vị khối lượng nguyên tử u là đúng?
- A
u bằng khối lượng của một nguyên tử \({}_1^1H\)
- B
u bằng khối lượng của hạt nhân nguyên tử cacbon \({}_6^{12}C\)
- C
u bằng 1/12 khối lượng của hạt nhân nguyên tử cacbon \({}_6^{12}C\)
- D
u bằng 1/12 khối lượng một nguyên tử \({}_6^{12}C\)
Đáp án: D
Lời giải chi tiết:
Đơn vị của khối lượng hạt nhân: u
Đơn vị u có giá trị bằng \(\frac{1}{{12}}\) khối lượng nguyên tử của đồng vị \(_6^{12}C\); cụ thể \(1{\rm{ }}u = \frac{1}{{12}}{m_C} = 1,{66055.10^{ - 27}}kg\)
Câu hỏi 21 :
Dao động điện từ trong mạch là dao động điều hòa. Khi hiệu điện thế giữa hai đầu cuộn cảm bằng \(u = 6\sqrt 3 mV\) thì cường độ dòng điện trong mạch bằng \(i{\rm{ }} = {\rm{ }}1,8{\rm{ }}mA\) . Còn khi hiệu điện thế giữa hai đầu cuộn cảm bằng \(u = 6mV\) thì cường độ dòng điện trong mạch bằng \(i{\rm{ }} = {\rm{ }}2,4{\rm{ }}mA\). Biết độ tự cảm của cuộn dây \(L{\rm{ }} = {\rm{ }}5mH\)năng lượng dao động điện từ trong mạch bằng:
- A
\({2,25.10^{ - 8}}J\)
- B
\({1,755.10^{ - 8}}J\)
- C
\({3,51.10^{ - 8}}J\)
- D
\({4,5.10^{ - 8}}J\)
Đáp án: B
Phương pháp giải:
Áp dụng biểu thức xác định năng lượng điện từ: \(W = \dfrac{1}{2}C{u^2} + \dfrac{1}{2}L{i^2}\)
Lời giải chi tiết:
Ta có năng lượng điện từ trong mạch được bảo toàn: \(W = \dfrac{1}{2}C{u^2} + \dfrac{1}{2}L{i^2} = h/s\)
Ta suy ra:
\(\begin{array}{l}\dfrac{1}{2}C{u_1}^2 + \dfrac{1}{2}L{i_1}^2 = \dfrac{1}{2}C{u_2}^2 + \dfrac{1}{2}L{i_2}^2\\ \Rightarrow C{u_1}^2 + L{i_1}^2 = C{u_2}^2 + L{i_2}^2\\ \Leftrightarrow C = \dfrac{{L({i_2}^2 - {i_1}^2)}}{{{u_1}^2 - {u_2}^2}} = \dfrac{{{{5.10}^{ - 3}}({{({{2,4.10}^{ - 3}})}^2} - {{({{1,8.10}^{ - 3}})}^2})}}{{{{\left( {6\sqrt 3 {{.10}^{ - 3}}} \right)}^2} - {{\left( {{{6.10}^{ - 3}}} \right)}^2}}} = {1,75.10^{ - 4}}C = 175\mu C\end{array}\)
+ Năng lượng dao động điện từ trong mạch: \(W = \dfrac{1}{2}C{u_1}^2 + \dfrac{1}{2}L{i_1}^2 = \dfrac{1}{2}{1,75.10^{ - 4}}.{\left( {6\sqrt 3 {{.10}^{ - 3}}} \right)^2} + \dfrac{1}{2}{5.10^{ - 3}}{({1,8.10^{ - 3}})^2} = {1,755.10^{ - 8}}J\)
Câu hỏi 22 :
Một mạch dao động LC đang có dao động điện từ tự do. Hiệu điện thế cực đại giữa hai bản tụ là \({U_0} = 4V\) . Tại thời điểm mà năng lượng từ trường bằng ba lần năng lượng điện trường thì hiệu điện thế giữa hai bản tụ bằng
- A
2 V
- B
1 V
- C
3 V
- D
2,4 V
Đáp án: A
Phương pháp giải:
Sử dụng biểu thức tính năng lượng điện từ: \(W = {W_t} + {W_d} = \dfrac{1}{2}CU_0^2\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{{\rm{W}}_L} + {{\rm{W}}_C} = {\rm{W}}\\{{\rm{W}}_L}{\rm{ = 3}}{{\rm{W}}_C}\end{array} \right.\\ \Rightarrow 4{W_C} = {\rm{W}} \Leftrightarrow 4.\dfrac{{C{u^2}}}{2} = \dfrac{{CU_0^2}}{2}\\ \Rightarrow u = \dfrac{{{U_0}}}{2} = 2V\end{array}\).
Câu hỏi 23 :
Mạch dao động LC gồm một cuộn dây có độ tự cảm \(30\mu H\), một tụ điện có điện dung \(3000{\rm{ }}pF\). Điện trở thuần của mạch dao động là \(1\Omega \). Để duy trì dao động điện từ trong mạch với điện lượng cực đại trên tụ là \(18{\rm{ }}nC\) phải cung cấp cho mạch một năng lượng điện có công suất là
- A
1,80 W
- B
1,80 mW
- C
0,18 W
- D
5,5 mW
Đáp án: B
Phương pháp giải:
+ Sử dụng biểu thức năng lượng điện từ: \({\rm{W}} = \dfrac{1}{2}CU_0^2 = \dfrac{1}{2}LI_0^2 = \dfrac{1}{2}\dfrac{{Q_0^2}}{C}\)
+ Sử dụng công thức tính công suất: \(P = {I^2}R = \dfrac{{I_0^2}}{2}R\)
Lời giải chi tiết:
Ta có: \({\rm{W}} = \dfrac{{Q_0^2}}{{2C}} = \dfrac{{LI_0^2}}{2} \Rightarrow I_0^2 = \dfrac{{Q_0^2}}{{LC}}\)
Công suất cần cung cấp:
\(P = \dfrac{1}{2}I_0^2R = \dfrac{1}{2}.\dfrac{{Q_0^2}}{{LC}}.R = \dfrac{1}{2}.\dfrac{{{{18}^2}{{.10}^{ - 18}}}}{{{{30.10}^{ - 6}}{{.3000.10}^{ - 12}}}}.1 = {1,8.10^{ - 3}} = 1,8mW\)
Câu hỏi 24 :
Một mạch dao động lí tưởng gồm cuộn cảm thuần có độ tư cảm \(L\) và tụ điện có điện dung \(C\) đang có dao động điện từ tự do. Ở thời điểm \(t\), dòng điện qua cuộn dây có cường độ bằng \(0\) thì ở thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2}\)
- A
dòng điện qua cuộn dây có cường độ bằng \(0\)
- B
điện tích trên một bản tụ có độ lớn cực đại
- C
năng lượng điện trường bằng \(0\)
- D
điện tích trên một bản tụ có giá trị bằng một nửa giá trị cực đại của nó
Đáp án: C
Phương pháp giải:
Xác định giá trị i, u, q tại thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2}\)
Lời giải chi tiết:
Ta có, tại thời điểm t cường độ dòng điện \(i = 0A\) (có thể ở vị trí 1 hoặc 2 như hình vẽ)
Ở thời điểm \(t + \dfrac{{\pi \sqrt {LC} }}{2} = t + \dfrac{T}{4}\)
+ Ứng với vị trí 1 => tại thời điểm \(t + \dfrac{T}{4}\) cường độ dòng điện \(i = {I_0}\)
+ Ứng với vị trí 2 => tại thời điểm \(t + \dfrac{T}{4}\) cường độ dòng điện \(i = - {I_0}\)
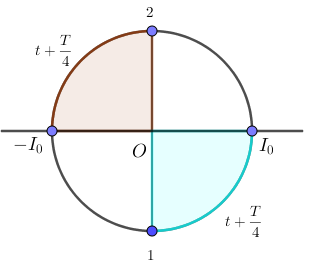
\(\Rightarrow \left| i \right| = {I_0}\) và \(u = 0,q = 0\)
\( \Rightarrow \) Năng lượng điện trường: \({{\rm{W}}_d} = \dfrac{{{q^2}}}{{2C}} = 0\)
Câu hỏi 25 :
Một mạch dao động điện từ LC lí tưởng gồm cuộn cảm thuần có độ tự cảm 5μH và tụ điện có điện dung 5 μF. Trong mạch có dao động điện từ tự do. Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên một bản tụ điện có độ lớn cực đại là
- A
5π.10-6
- B
2,5π.10-6s
- C
10π.10-6
- D
10-6
Đáp án: A
Phương pháp giải:
+ Áp dụng công thức tính chu kì dao động của mạch LC: \(T = 2\pi \sqrt {LC} \)
+ Sử dụng trục thời gian suy ra từ vòng tròn
Lời giải chi tiết:
Ta có
+ Chu kì dao động của mạch: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{5.10}^{ - 6}}{{.5.10}^{ - 6}}} = 10\pi {.10^{ - 6}}{\rm{s}}\)
+ Khoảng thời gian giữa hai lần liên tiếp mà điện tích trên bản tụ có độ lớn cực đại là :
\(\frac{T}{2} = \frac{{10\pi {{.10}^{ - 6}}}}{2} = 5\pi {.10^{ - 6}}s\)
Câu hỏi 26 :
Theo mẫu nguyên tử Bo, mức năng lượng của trạng thái dừng thứ n của nguyên tử Hidro được xác định theo công thức \({E_n} = - \dfrac{{13,6}}{{{n^2}}}\left( {eV} \right);\left( {n = 1,2,3...} \right)\) Gọi R1 là bán kính quỹ đạo của e khi nguyên tử Hidro ở tạng thái dừng L. Khi nguyên tử ở trạng thái dừng ứng với bán kính bằng 9R1 thì tỷ số bước sóng lớn nhất và bước sóng nhỏ nhất của photon mà nguyên tử Hidro có thể phát xạ là:
- A
\(\dfrac{{32}}{5}\)
- B
\(\dfrac{{135}}{7}\)
- C
\(\dfrac{{125}}{{44}}\)
- D
\(\dfrac{{875}}{{11}}\)
Đáp án: D
Phương pháp giải:
Áp dụng công thức xác định mức năng lượng của photon: \({E_n} = - \dfrac{{13,6}}{{{n^2}}}\left( {eV} \right);\left( {n = 1,2,3...} \right)\)
Lời giải chi tiết:
R1 là bán kính quỹ đạo e ứng với trạng thái dừng L vậy \({r_1} = {2^2}{r_0}\)
Khi bán kính quỹ đạo là 9R1 ta có \(r = 9{r_1} = 9.4{r_0} = 36{r_0} = > n = 6\) ứng với trạng thái dừng P
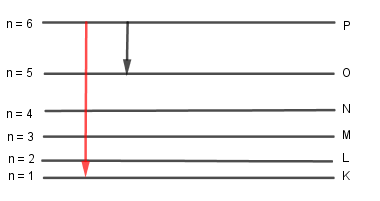
Bước sóng lớn nhất mà photon này có thể phát xạ ra khi nó chuyển mức năng lượng từ trạng thái P về trạng thái K là \(E = {E_P} - {E_0} = \dfrac{{{E_0}}}{{{6^2}}} - {E_0} = \dfrac{{35}}{{36}}{E_0} = \dfrac{{hc}}{{{\lambda _{max}}}} = > {\lambda _{max}} = \dfrac{{hc}}{{\dfrac{{35}}{{36}}{E_0}}}\)
Bước sóng ngắn nhất photon này có thể phát xạ ra khi nó chuyển mức năng lượng từ trạng thái P về trạng thái O là \(E = {E_P} - {E_O} = \dfrac{{{E_0}}}{{{6^2}}} - \dfrac{{{E_0}}}{5} = \dfrac{{11}}{{900}}{E_0} = \dfrac{{hc}}{{{\lambda _{\min }}}} = > {\lambda _{\min }} = \dfrac{{hc}}{{\dfrac{{11}}{{900}}{E_0}}}\)
Tỷ số giữa bước sóng ngắn lớn nhất và dài nhất là \(\dfrac{{{\lambda _{\min }}}}{{{\lambda _{max}}}} = \dfrac{{\dfrac{{hc}}{{\dfrac{{35}}{{36}}{E_0}}}}}{{\dfrac{{hc}}{{\dfrac{{11}}{{900}}{E_0}}}}} = \dfrac{{35}}{{36}}.\dfrac{{900}}{{11}} = \dfrac{{875}}{{11}}\)
Câu hỏi 27 :
Trong mạch dao động LC có điện trở thuần không đáng kể, chu kỳ dao động của mạch là \(T{\rm{ }} = {\rm{ }}{10^{ - 6}}s\), khoảng thời gian ngắn nhất để năng lượng điện trường lại bằng năng lượng từ trường :
- A
\({2,5.10^{ - 5}}s\)
- B
\({10^{ - 6}}s\)
- C
\({5.10^{ - 7}}s\)
- D
\({2,5.10^{ - 7}}s\)
Đáp án: D
Phương pháp giải:
+ Vận dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \dfrac{1}{2}C{U_0}^2 = \dfrac{{{Q_0}^2}}{{2C}} = \dfrac{{LI{{_0^{}}^2}}}{2}\)
+ Vận dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)
Lời giải chi tiết:
Đề cho: \({W_C} = {W_L}\)
W = WC + WL = \(\dfrac{{{q^2}}}{{2C}}\) + \(\dfrac{{L{i^2}}}{2}\)
<=>\(\dfrac{{{q_0}^2}}{{2C}}\) =\(\dfrac{{{q^2}}}{{2C}}\) +\(\dfrac{{{q^2}}}{{2C}}\)
<=> \(q = \dfrac{{\sqrt 2 }}{2}{q_0}\)
Hình vẽ vòng lượng gíác cho ta góc quét từ lúc năng lượng điện trường cực đại đến năng lượng điện trường bàng năng lượng từ rường là: \(\Delta \varphi = \dfrac{\pi }{4}\)
Câu hỏi 28 :
Góc chiết quang của lăng kính bằng A = 60. Chiếu một tia sáng trắng vào mặt bên của lăng kính theo phương vuông góc với mặt phẳng phân giác của góc chiết quang. Đặt một màn quan sát, sau lăng kính, song song với mặt phẳng phân giác của góc chiết quang của lăng kính và cách mặt này 2m. Chiết suất của lăng kính đối với tia đỏ là nd = 1,5 và đối với tia tím là nt = 1,56 . Độ rộng của quang phổ liên tục trên màn quan sát bằng
- A
6,28 mm
- B
12,57 mm
- C
9,30 mm
- D
0,72 mm
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính bề rộng quang phổ:
\(\Delta x = {x_t} - {x_d} = \left( {{n_t} - {n_d}} \right)LA\)
Câu hỏi 29 :
Trong thí nghiệm Y‒âng về giao thoa ánh sáng, khoảng cách giữa hai khe là \(1,2 mm\), bước sóng của ánh sáng đơn sắc dùng trong thí nghiệm là \(600 nm\). Trên màn quan sát, khoảng cách từ vân sáng bậc \(1\) đến vân tối thứ \(6\) ở cùng một phía so với vân sáng trung tâm là \(0,45 cm\). Khoảng cách từ hai khe tới màn quan sát là
- A
\(1,0 m\).
- B
\(1,26 m\).
- C
\(1,76 m\).
- D
\(2,0 m\).
Đáp án: D
Phương pháp giải:
Vị trí vân sáng: xs=ki
Vị trí vân tối: xt=(k+0,5)i
Công thức tính khoảng vân\(i = \dfrac{{\lambda D}}{a}\)
Lời giải chi tiết:
Ta có,
+ Vị trí vân sáng bậc 1: \(x_{s_1}=i\)
+ Vị trí vân tối thứ 6: \(x_{t_6}=\dfrac{11i}{2}\)
=> khoảng cách từ vân sáng bậc 1 đến vân tối thứ 6 ở cùng phía so với vân trung tâm:
\(d =\dfrac{11i}{2} - i=4,5i =4,5 mm\)
=> \(i= 1 mm\);
Lại có: \(i = \dfrac{{\lambda D}}{a} \to D = \dfrac{{ai}}{\lambda } =2m \)
Câu hỏi 30 :
Trong thí nghiệm giao thoa sóng ánh sáng với khoảng cách giữa hai khe là \(a = 1,2mm\). Khoảng cách từ mặt phẳng chứa hai khe tới màn là \(D = 3m\). Hai khe được chiếu sáng bởi ánh sáng đơn sắc có bước sóng \(\lambda = 0,44\mu m\). Vị trí vân sáng bậc hai trên màn là:
- A
\( \pm 2,2mm\)
- B
\( \pm 1,1mm\)
- C
\( \pm 3,3mm\)
- D
\( \pm 4,4mm\)
Đáp án: A
Phương pháp giải:
+ Áp dụng công thức tính khoảng vân: \(i = \dfrac{{\lambda D}}{a}\)
+ Sử dụng công thức xác định vị trí vân sáng: \({x_S} = {\rm{ }}ki\)
Lời giải chi tiết:
Ta có:
+ Khoảng vân i: \(i = \dfrac{{\lambda D}}{a} = \dfrac{{{{0,44.10}^{ - 6}}.3}}{{{{1,2.10}^{ - 3}}}} = {1,1.10^{ - 3}}m = 1,1mm\)
+ Vị trí vân sáng bậc 2 trên màn ứng với \(k = \pm 2\) là: \({x_{{S_2}}} = \pm 2i = \pm 2.1,1 = \pm 2,2mm\)
Câu hỏi 31 :
Trong thí nghiệm giao thoa ánh sáng đơn sắc với hai khe I-âng, cho D = 1,5m. Nguồn sáng S phát ra ánh sáng đơn sắc có bước sóng λ. Khoảng cách từ S đến mặt phẳng hai khe là d = 60cm. Khoảng vân đo được trên màn bằng i = 3mm. Điểm M cách vân trung tâm một đoạn x = 3mm về phía S2. Cho S dời theo phương song song với S1S2 về phía S2 một đoạn 3mm. Khi đó tại M cho vân sáng hay vân tối bậc mấy?
- A
Vân tối thứ 4
- B
Vân tối thứ 2
- C
Vân sáng bậc 1
- D
Vân sáng bậc 2
Đáp án: A
Phương pháp giải:
+ Vận dụng công thức khi dịch chuyển nguồn sáng (xem lí thuyết phần 1)
+ Xác định vị trí vân sáng - tối trên màn
Lời giải chi tiết:
Ta có, khi dịch chuyển nguồn sáng S theo phương song song về phía S2
Câu hỏi 32 :
Thí nghiệm giao thoa ánh sáng I-âng. Chiếu hai khe ánh sáng đơn sắc có bước sóng \({\lambda _1} = 0,6\mu m\)thì trên màn quan sát, ta thấy khoảng cách giữa 6 vân sáng liên tiếp là 9mm. Nếu chiếu hai khe đồng thời ba bức xạ \({\lambda _1};{\lambda _2} = 0,48\mu m;{\lambda _3} = 0,4\mu m\)và đặt khe của máy quang phổ tại đúng vị trí cách vận trung tâm 10,8mm thì trên màn ảnh sẽ thấy:
- A hai vạch sáng ứng với \({\lambda _1}\) và \({\lambda _3}\)
- B cả vạch sáng ứng với \({\lambda _1},{\lambda _2},{\lambda _3}\)
- C hai vạch sáng ứng với \({\lambda _2}\) và \({\lambda _3}\)
- D hai vạch sáng ứng với \({\lambda _1}\) và \({\lambda _2}\)
Đáp án: A
Phương pháp giải:
+ Vị trí vân sáng trên màn quan sát: \({x_s} = k.i = \dfrac{{k.\lambda D}}{a};k \in Z\)
+ Khoảng vân là khoảng cách giữa hai vân sáng liên tiếp.
+ Tại M có: \(\dfrac{{{x_M}}}{i} = k;k \in Z\) thì tại M là vân sáng bậc k.
Lời giải chi tiết:
+ Khi chiếu bức xạ có bước sóng \({\lambda _1} = 0,6\mu m\), khoảng cách giữa 6 vân sáng liên tiếp là 9mm:
\(5.{i_1} = 9mm \Rightarrow i = 1,8mm \Rightarrow \dfrac{{{\lambda _1}D}}{a} = 1,8 \Rightarrow \dfrac{D}{a} = 3\)
+ Vị trí vân sáng của các bức xạ: \(\left\{ \begin{array}{l}{i_1} = 1,8\,\,\left( {mm} \right)\\{i_2} = \dfrac{{{\lambda _2}D}}{a} = 0,48.3 = 1,44\,\,\left( {mm} \right)\\{i_3} = \dfrac{{{\lambda _3}D}}{a} = 0,4.3 = 1,2\,\,\left( {mm} \right)\end{array} \right.\)
+ Tại \(x = 10,8mm \Rightarrow \left\{ \begin{array}{l}\dfrac{x}{{{i_1}}} = \dfrac{{10,8}}{{1,8}} = 6 \in Z\\\dfrac{x}{{{i_2}}} = \dfrac{{10,8}}{{1,44}} = 7,5 \notin Z\\\dfrac{x}{{{i_3}}} = \dfrac{{10,8}}{{1,2}} = 9 \in Z\end{array} \right.\)
Vậy tại vị trí cách vân trung tâm 10,8mm có hai vạch sáng ứng với \({\lambda _1}\) và \({\lambda _3}\)
Câu hỏi 33 :
Một nguồn sáng phát ra đồng thời hai ánh sáng đơn sắc màu đỏ có bước sóng \({\lambda _1} = 0,72\mu m\) và bức xạ màu cam có bước sóng \({\lambda _2}\) \(\left( {0,59\mu m \le {\lambda _2} \le 0,65\mu m} \right)\) chiếu vào khe Y-âng. Trên màn người ta quan sát thấy giữa vân sáng cùng màu và gần nhất so với vân trung tâm có 7 vân màu cam. Bước sóng của bức xạ \({\lambda _2}\) là:
- A
\(0,62\mu m\)
- B
\(0,63\mu m\)
- C
\(0,59\mu m\)
- D
\(0,60\mu m\)
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết về hai vân sáng trùng nhau trong giao thoa ánh sáng
+ Hai vân trùng nhau : \({x_1} = {\rm{ }}{x_2}\)
+ Vị trí vân sáng: \({x_S} = ki = k\dfrac{{\lambda D}}{a}\)
Lời giải chi tiết:
Tại vị trí vân sáng cùng màu với vân trung tâm đó có:
+ Vân sáng bậc \(8\) của \({\lambda _2}\)
+ Vân sáng bậc \(k\) của \({\lambda _1}\)
\(\begin{array}{l} \Rightarrow 8{\lambda _2} = k.{\lambda _1} \Leftrightarrow 8{\lambda _2} = k.0,72\\ \Rightarrow {\lambda _2} = 0,09k\left( {\mu m} \right)\end{array}\)
Vì: \(0,59\mu m \le {\lambda _2} \le 0,65\mu m\)
\(\begin{array}{l} \Leftrightarrow 0,59 \le 0,09k \le 0,65\\ \Leftrightarrow 6,55 \le k \le 7,22\\ \Rightarrow k = 7\\ \Rightarrow {\lambda _2} = 0,09.7 = 0,63\mu m\end{array}\)
Câu hỏi 34 :
Một chùm bức xạ điện từ có tần số 24.1014 Hz. Cho vận tốc ánh sáng trong chân không c = 3.108 m/s.Trong không khí (chiết suất lấy bằng 1), chùm bức xạ này có bước sóng bằng bao nhiêu và thuộc vùng nào trong thang sóng điện từ?
- A
λ= 0,48 mm; vùng ánh sáng nhìn thấy.
- B
λ= 48 pm; vùng tia X.
- C
λ= 1,25 mm; vùng hồng ngoại.
- D
λ= 125 nm; vùng tử ngoại.
Đáp án: D
Phương pháp giải:
+ Áp dụng công thức tính bước sóng: \(\lambda = \frac{c}{f}\)
+ Sử dụng thang sóng điện từ
Lời giải chi tiết:
Ta có:
\(\lambda = \frac{c}{f} = \frac{{{{3.10}^8}}}{{{{24.10}^{14}}}} = {125.10^{ - 9}}m\) thuộc vùng tử ngoại
Câu hỏi 35 :
Trong thí nghiệm giao thoa Y-âng, nguồn S phát ánh sáng đơn sắc có bước sóng \(\lambda \) người ta đặt màn quan sát cách mặt phẳng hai khe một khoảng D thì khoảng vân là 1mm. Khi khoảng cách từ màn quan sát đến mặt phẳng hai khe lần lượt là \(D + \Delta D\) hoặc \(D - \Delta D\) thì khoảng vân thu được trên màn tương ứng là \(2i\) và \(i.\) Nếu khoảng cách từ màn quan sát đến mặt phẳng hai khe là \(D + 3\Delta D\) thì khoảng vân trên màn là:
- A
3 mm
- B
2,5 mm
- C
2 mm
- D
4 mm
Đáp án: C
Phương pháp giải:
Vận dụng biểu thức tính khoảng vân \(i = \dfrac{{\lambda D}}{a}\)
Lời giải chi tiết:
Ta có: \({i_1} = \dfrac{{\lambda D}}{a} = 1mm\)
Khi khoảng cách từ màn quan sát đến mặt phẳng hai khe thay đổi :
\(\begin{array}{l}{i_2} = 2i = \dfrac{{D + \Delta D}}{a}\lambda (1)\\{i_3} = i = \dfrac{{D - \Delta D}}{a}\lambda (2)\\\dfrac{{(1)}}{{(2)}} \Rightarrow \Delta D = \dfrac{D}{3}(3)\end{array}\)
Nếu khoảng cách từ màn quan sát đến mặt phẳng hai khe là \(D + 3\Delta D\):
\( \Rightarrow i' = \dfrac{{D + 3\Delta D}}{a}\lambda = \dfrac{{D + D}}{a}\lambda = 2{i_1} = 2.1 = 2mm\)
Câu hỏi 36 :
Một bức xạ truyền trong không khí với chu kỳ $8,{25.10^{ - 16}}s$. Bức xạ này thuộc vùng nào của thang sóng điện từ?
- A
Tia X.
- B
Vùng tử ngoại.
- C
Vùng hồng ngoại.
- D
Vùng ánh sáng nhìn thấy
Đáp án: B
Phương pháp giải:
+ Vận dụng biểu thức: \(\lambda = cT\)
+ Sử dụng thang sóng điện từ:
Lời giải chi tiết:
Bức xạ có bước sóng: $\lambda = cT = {3.10^8}.8,{25.10^{ - 16}} = 2,{475.10^{ - 7}}m = 0,2475\mu m$
=> Bức xạ này thuộc vùng tử ngoại
Câu hỏi 37 :
Catốt của một tế bào quang điện làm bằng Xeđi được chiếu bởi bức xạ có \(\lambda = {\rm{ }}0,3975\mu m\) . Cho cường độ dòng quang điện bão hòa \(2\mu A\) và hiệu suất quang điện H = 0,5%. Số photon tới catốt trong mỗi giây là
- A
1,5.1015 photon
- B
1015 photon
- C
2,5.1015 photon
- D
1012 photon
Đáp án: C
Phương pháp giải:
+ Áp dụng công thức tính hiệu suất lượng tử:
\(H = \frac{{{n_e}}}{{{n_p}}}100\% \)
+ Áp dụng công thức tính số electron bứt ra khỏi catốt trong 1s:
\({n_e} = \frac{{{N_e}}}{t} = \frac{{{I_{bh}}}}{e}\)
Lời giải chi tiết:
Ta có:
+ Hiệu suất lượng tử:
\(H = \frac{{{n_e}}}{{{n_p}}}100\% \)
Mặt khác, ta có:
\({n_e} = \frac{{{N_e}}}{t} = \frac{{{I_{bh}}}}{e}\)
\( \to {n_p} = \frac{{{n_e}}}{H} = \frac{{{I_{bh}}}}{{eH}} = \frac{{{{2.10}^{ - 6}}}}{{1,{{6.10}^{ - 19}}.\frac{{0,5}}{{100}}}} = 2,{5.10^{15}}\)
=> Số photon tới catốt trong mỗi giây là: np
Câu hỏi 38 :
Một chất có khả năng phát quang ánh sáng màu đỏ và ánh sáng màu lục. Nếu dùng tia tử ngoại để kích thích sự phát quang của chất đó thì ánh sáng phát quang có thể có màu nào ?
- A
Màu đỏ
- B
Màu vàng
- C
Màu lục
- D
Màu lam
Đáp án: B
Phương pháp giải:
+ Vận dụng tính chất của tia tử ngoại
+ Vận dụng công thức trộn màu sơ cấp
Lời giải chi tiết:
Ta có:
+ Khi chiếu ánh sáng tử ngoại vào thì chất đó phát ra cả ánh sáng màu lục và màu đỏ
+ Lục + đỏ = vàng
Câu hỏi 39 :
Chiếu một bức xạ có bước sóng λ= 0, 48𝜇m lên một tấm kim loại có công thoát A = 2,4.10-19J. dùng màn chắn tách ra một chùm hẹp các êlectron quang điện và hướng chúng bay theo chiều véc tơ cường độ điện trường có E = 1000 V/m. Quãng đường tối đa mà êlectron chuyển động được theo chiều véc tơ cường độ điện trường xấp xỉ là:
- A
0,83cm
- B
0,37cm
- C
1,53cm
- D
0,109cm
Đáp án: D
Phương pháp giải:
Áp dụng công thức Anh – xtanh và lí thuyết về chuyển động thẳng biến đổi đều
Công thức Anh – xtanh:
\(\frac{{hc}}{\lambda } = A + \frac{1}{2}mv_0^2\)
Lực điện: F = qE
Công thức của chuyển động thẳng biến đổi đều:
\({v^2} - v_0^2 = 2as\)
Lời giải chi tiết:
+ Theo công thức Anh - xtanh :
\(\dfrac{{hc}}{\lambda } = A + \dfrac{1}{2}m.{v_0}^2 \Rightarrow {v_0}^2 = \dfrac{2}{m}\left( {\dfrac{{hc}}{\lambda } - A} \right)\) \(({m_e} = 9,{1.10^{ - 31}}kg)\)
+ Ta có:
\(a = \dfrac{F}{m} = \dfrac{{qE}}{m}\)
+ Chuyển động của e là chuyển động chậm dần đều với vận tốc đầu v0 và gia tốc a
Electron dừng v = 0
\( \Leftrightarrow {0^2}-{\rm{ }}{v_0}^2 = {\rm{ }}2as \Rightarrow s = - \dfrac{{{v_0}^2}}{{2a}} = - \dfrac{{\dfrac{2}{m}\left( {\dfrac{{hc}}{\lambda } - A} \right)}}{{2.\dfrac{{qE}}{m}}} = - \dfrac{{\dfrac{{hc}}{\lambda } - A}}{{qE}} \Rightarrow s = 0,109cm\)
Câu hỏi 40 :
Nguyên tử hiđrô được kích thích để chuyển lên quỹ đạo dừng M. Khi nó chuyển về các trạng thái dừng có mức năng lượng thấp hơn thì sẽ phát ra:
- A
một bức xạ
- B
hai bức xạ
- C
ba bức xạ
- D
bốn bức xạ
Đáp án: C
Câu hỏi 41 :
Hạt nhân đơteri \({}_1^2D\)có năng lượng liên kết là \(2,2356 MeV\). Năng lượng liên kết riêng của hạt nhân này bằng
- A
\(1,1178 MeV/nuclon\).
- B
\(4,4712 MeV/nuclon\).
- C
\(2,2356 MeV/nuclon\).
- D
\(0,7452 MeV/nuclon\).
Đáp án: A
Phương pháp giải:
Năng lượng liên kết riêng của hạt nhân: \({{\rm{W}}_{LKR}} = \dfrac{{{{\rm{W}}_{LK}}}}{A}\)
Lời giải chi tiết:
\({{\rm{W}}_{LKR}} = \dfrac{{{{\rm{W}}_{LK}}}}{A} = \dfrac{{2,2356}}{2} = \)\(1,1178(MeV)\)
Câu hỏi 42 :
Khối lượng của nguyên tử nhôm \(_{13}^{27}Al\) là \(26,9803u\). Khối lượng của proton là \(1,00728u\) và khối lượng của notron là \(1,00866u\). Độ hụt khối của hạt nhân nhôm là:
- A
\(0,242665u\)
- B
\(0,23558u\)
- C
\(0,23548u\)
- D
\(0,23544u\)
Đáp án: B
Phương pháp giải:
Vận dụng biểu thức xác định độ hụt khối của hạt nhân X: \(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)
Lời giải chi tiết:
Ta có, hạt nhân \(_{13}^{27}Al\) có: \(\left\{ \begin{array}{l}Z = 13\\N = A - Z = 27 - 13 = 14\end{array} \right.\)
Độ hụt khối của hạt nhân: \(_{13}^{27}Al\) là:
\(\begin{array}{l}\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_{Al}}\\ = 13.1,00728u + 14.1,00866u - 26,9803u\\ = 0,23558u\end{array}\)
Câu hỏi 43 :
Cho phản ứng hạt nhân \({}_{17}^{37}Cl + p \to {}_{18}^{37}{\rm{Ar}} + {}_0^1n\) , khối lượng của các hạt nhân là mAr = 36,956889u, mCl = 36,956563 u; mn = 1,008670u , mp = 1,007276u; 1u = 931,5 MeV/c2. Năng lượng mà phản ứng này tỏa ra hoặc thu vào là
- A Tỏa ra 1,60218 MeV
- B Thu vào 1,60218 MeV
- C Tỏa ra 2,562112.10-19 J.
- D Thu vào 2,562112.10-19 J.
Đáp án: B
Phương pháp giải:
Áp dụng công thức năng lượng tỏa ra hay thu vào của phản ứng hạt nhân
W = (mtr - ms).c2.
Nếu W >0 thì phản ứng tỏa năng lượng; W < 0 thì phản ứng thu năng lượng
Lời giải chi tiết:
Áp dụng công thức năng lượng tỏa ra hay thu vào của phản ứng hạt nhân
W = (mtr - ms).c2 = (36,956563 + 1,007276- 36,956889-1,008670).931,5
= -1,60218 MeV
Vậy phản ứng thu năng lượng
Câu hỏi 44 :
Dùng một proton có động năng 5,58MeV bắn phá hạt nhân \(_{11}^{23}Na\) đứng yên, sinh ra hạt \(\alpha \) và hạt nhân X và không kèm theo bức xạ gamma. Biết năng lượng tỏa ra trong phản ứng chuyển hết thành đọng năng của các hạt tạo thành, động năng của hạt \(\alpha \) là 6,6MeV và động năng của hạt X là 2,648MeV. Cho khối lượng các hạt tính theo u bằng số khối. Góc tạo bởi hướng chuyển động của hạt \(\alpha \) và hướng chuyển động của hạt proton là
- A
\({147^0}\)
- B
\({148^0}\)
- C
\({150^0}\)
- D
\({120^0}\)
Đáp án: C
Lời giải chi tiết:
\(_1^1p + _{11}^{23}Na \to _2^4\alpha + _{10}^{20}X\)
Gọi \(\varphi = \widehat {\overrightarrow {{v_\alpha }} ;\overrightarrow {{v_p}} }\)
Câu hỏi 45 :
Đồng vị \(^{210}Po\) phóng xạ \(\alpha \) và biến thành một hạt nhân chì \(^{206}Pb\). Ban đầu có \(0,168\left( g \right)Po\), sau một chu kì bán rã, thể tích của khí Heli sinh ra ở điều kiện tiêu chuẩn (1mol khí trong điều kiện tiêu chuẩn chiếm một thể tích \(22,4l\)) là:
- A
\(0,00899ml\)
- B
\(8,96ml\)
- C
\(0,89ml\)
- D
\(0,089ml\)
Đáp án: B
Phương pháp giải:
+ Khối lượng hạt nhân mẹ đã phân rã: \(\Delta {m_{m{\rm{e}}}}{\rm{ }} = {m_0}(1 - {2^{ - \dfrac{t}{T}}})\)
+ Sử dụng công thức tính khối lượng hạt nhân con: \({m_{con}} = \dfrac{{\Delta {m_{me}}}}{{{A_{me}}}}.{A_{con}}\)
+ Xác định số mol Heli được tạo thành
+ Sử dụng biểu thức tính thể tích khí ở điều kiện tiêu chuẩn: \(V = n.22,4\left( l \right)\)
Lời giải chi tiết:
Ta có: \(^{210}Po{ \to ^{206}}Pb{ + ^4}He\)
=> Số mol chì được tạo ra chính bằng số mol Heli
Lại có, khối lượng chì được tạo ra sau một chu kì bán rã là:
\({m_{Pb}} = \dfrac{{\Delta {m_{Po}}}}{{{A_{Po}}}}.{A_{Pb}} = {m_0}\dfrac{{{A_{Pb}}}}{{{A_{Po}}}}(1 - {2^{\dfrac{t}{T}}}) = 0,168\dfrac{{206}}{{210}}(1 - {2^{ - \dfrac{T}{T}}}) = 0,0824g\)
=> Số mol chì được tạo thành trong thời gian đó là: \(n = \dfrac{{{m_{Pb}}}}{{{A_{Pp}}}} = \dfrac{{0,00824}}{{206}} = {4.10^{ - 4}}\left( {mol} \right)\)
=> Thể tích khí Heli sinh ra ở điều kiện tiêu chuẩn sau một chu kì bán rã là:
\(V = n.22,4 = {4.10^{ - 4}}.22,4 = 8,{96.10^{ - 3}}l = 8,96ml\)
Câu hỏi 46 :
Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn phát ra ánh sáng trắng có bước sóng từ \(380nm\) đến \(760nm\). Trên màn quan sát, tại điểm \(M\) có đúng \(4\) bức xạ cho vân sáng có bước sóng \(390nm\); \(520nm\);\({\lambda _1}\) và \({\lambda _2}\). Tổng giá trị gần nhất với:
- A
\(10000nm\)
- B
\(890nm\)
- C
\(1069nm\)
- D
\(943nm\)
Đáp án: C
Phương pháp giải:
+ Sử dụng điều kiện vân sáng trùng nhau: \({k_1}{\lambda _1} = {k_2}{\lambda _2} = {k_3}{\lambda _3}\)
+ Sử dụng biểu thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
+ Sử dụng điều kiện chồng chập vân: \({x_{{d_{\left( k \right)}}}} > {x_{{t_{\left( {k + 1} \right)}}}}\)
Lời giải chi tiết:
Tại M có cùng lúc 4 vân sáng ứng với 4 bức xạ, nên ta có :
\(\begin{array}{*{20}{l}}{{x_M} = {k_1}.{i_1} = {k_2}.{i_2} = {k_3}.{i_3} = {k_4}.{i_4}}\\{ = > \frac{{{k_3}}}{{{k_4}}} = \frac{{{i_4}}}{{{i_3}}} = \frac{{{\lambda _4}}}{{{\lambda _3}}} = \frac{{520}}{{390}} = \frac{4}{3}}\end{array}\)
Ta có thể coi như ở đây có sự giao thoa của hệ vân mà khoảng vân bằng bội của \(4.{i_3}\) hoặc \(3{i_4}\) .
Tức là :
\(\begin{array}{*{20}{l}}{i' = 4.\frac{{{\lambda _3}.D}}{a} = 4.390.x = 1560x}\\{Khi(x = \frac{D}{a})}\end{array}\)
Điều kiện để có hai dải vân chồng chập lên nhau là :
\(\begin{array}{l}{x_{{d_{\left( k \right)}}}} > {x_{{t_{\left( {k + 1} \right)}}}}\\ \leftrightarrow k{i_d} > \left( {k + 1} \right){i_t}\\ \leftrightarrow k{\lambda _d} > \left( {k + 1} \right){\lambda _t}\end{array}\)
\(\begin{array}{*{20}{l}}{k.760 > (k + 1).380}\\{ = > k > 1}\end{array}\)
Xét với \(k{\rm{ }} = {\rm{ }}2\), thì:
\(i' = 2.4{i_3} = 8{i_3} = 2.3{i_4} = 6{i_4} = 3120x\)
Ta lập bảng để xét các giá trị thỏa mãn:
![]()
Vậy chọn các giá trị ứng với \(k{\rm{ }} = {\rm{ }}8,7,6,5\)
Thì \({\lambda _1} + {\lambda _2} = 624 + 445,71 \approx 1069nm\)
Câu hỏi 47 :
Cho chùm nơtron bắn phá đồng vị bền \(_{25}^{55}Mn\) ta thu được đồng vị phóng xạ \(_{25}^{56}Mn\). Đồng vị phóng xạ \(_{25}^{56}Mn\) có chu trì bán rã \(T{\rm{ }} = {\rm{ }}2,5h\) và phát xạ ra tia \({\beta ^ - }\). Sau quá trình bắn phá \(_{25}^{55}Mn\) bằng nơtron kết thúc người ta thấy trong mẫu trên tỉ số giữa số nguyên tử \(_{25}^{56}Mn\) và số nguyên tử \(_{25}^{55}Mn\) bằng \({10^{ - 10}}\) . Sau \(10\) giờ tiếp đó thì tỉ số giữa nguyên tử của hai loại hạt trên là:
- A
\({3,125.10^{ - 12}}\)
- B
\({6,25.10^{ - 12}}\)
- C
\({2,5.10^{ - 11}}\)
- D
\({1,25.10^{ - 11}}\)
Đáp án: B
Phương pháp giải:
Áp dụng định luật phóng xạ
Số nguyên tử còn lại sau phân rã: \(N = {N_0}{.2^{ - \dfrac{t}{T}}}\)
Lời giải chi tiết:
Số nguyên tử \(_{25}^{55}Mn\) sau khi ngừng quá trình bắn phá là không thay đổi, chỉ có số nguyên tử \(_{25}^{56}Mn\)phóng xạ thay đổi theo thời gian.
Ngay khi quá trình bắn phá kết thúc (t = 0), số nguyên tử \(_{25}^{55}Mn\) là N1, số nguyên tử \(_{25}^{56}Mn\) là N0, ta có: \({N_0} = \dfrac{{{N_1}}}{{{{10}^{10}}}}\)
Sau t = 10h = 4T, số nguyên tử \(_{25}^{56}Mn\) còn lại là:
Câu hỏi 48 :
Tiến hành thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát ra đồng thời hai ánh sáng đơn sắc có bước sóng l1 và l2. Trên màn, trong khoảng giữa hai vị trí có vân sáng trùng nhau liên tiếp có tất cả N vị trí mà ở mỗi vị trí đó có một bức xạ cho vân sáng. Biết l1 và l2 có giá trị nằm trong khoảng từ \(400 nm\) đến \(750 nm\). N không thể nhận giá trị nào sau đây?
- A
\(7\)
- B
\(8\)
- C
\(5\)
- D
\(6\)
Đáp án: B
Lời giải chi tiết:
Giả sử \({\lambda _1} < {\lambda _2}\).
Gọi số vân sáng của lamda1 giữa 2 vân sáng chung liên tiếp là \(n_1\) số vân sáng của \(\lambda_2\) giữa 2 vân sáng chung liên tiếp là \(n_2\)
Ta có N = n1 + n2 và \(({n_1} + 1){\lambda _1} = ({n_2} + 1){\lambda _2} \Rightarrow \dfrac{{{n_1} + 1}}{{{n_2} + 1}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}}\)(1)
Mặt khác, vì \(\lambda_1\) và \(\lambda_2\) trong khoảng \(400nm\) đến \(750nm\) nên \(\dfrac{{{\lambda _2}}}{{{\lambda _1}}} < \dfrac{{750}}{{400}} = 1,875\)(2)
Từ (1) và (2) suy ra \({n_2} < {n_1} < 1,875{n_2} + 0,875\)
Để ý thấy (n1 + 1) và (n2 + 1) phải là 2 số nguyên tố cùng nhau (UCLN phải bằng 1) để giữa 2 vân sáng chung không còn vân sáng chung nào khác. Ta có bảng sau:
Câu hỏi 49 :
Xét nguyên tử hiđrô theo mẫu nguyên tử Bo. Khi electron trong nguyên tử chuyển động tròn trên quỹ đạo dừng O thì có tốc độ \(\dfrac{v}{5}m/s\). Biết bán kính Bo là r0. Nếu electron chuyển động trên một quỹ đạo dừng với thời gian chuyển động hết một vòng là \(\dfrac{{128\pi {r_0}}}{v}(s)\) thì electron này đang chuyển động trên quỹ đạo?
- A
O
- B
M
- C
P
- D
N
Đáp án: D
Phương pháp giải:
+ Vận dụng biểu thức lực tính điện: \({F_d} = k\dfrac{{{q_1}{q_2}}}{{{r^2}}}\)
+ Vận dụng biểu thức lực hướng tâm: \({F_{ht}} = m{a_{ht}} = m\dfrac{{{v^2}}}{r}\)
+ Công thức bán kính quỹ đạo của Borh: \({r_n} = {n^2}{r_0}\)
Lời giải chi tiết:
Lực tĩnh điện giữa e và hạt nhân đóng vai trò lực hướng tâm, nên ta có:
\(\begin{array}{*{20}{l}}{\dfrac{{k.{e^2}}}{{{r^2}}} = \dfrac{{m.{v^2}}}{r} = > {v^2} = \dfrac{{k.{e^2}}}{{m.r}} = > v = \sqrt {\dfrac{{k.{e^2}}}{{m.{n^2}.{r_0}}}} = \dfrac{1}{n}.\sqrt {\dfrac{{k.{e^2}}}{{m.{r_0}}}} }\\{{v_K} = \sqrt {\dfrac{{k.{e^2}}}{{m.{r_0}}}} }\\{{v_O} = \dfrac{1}{5}.\sqrt {\dfrac{{k.{e^2}}}{{m.{r_0}}}} = \dfrac{{{v_K}}}{5} = a( = v/5)}\\{{v_n} = \dfrac{{{v_K}}}{n} = \dfrac{{5.a}}{n} = \dfrac{v}{n}}\end{array}\)
Chu kì chuyển động của hạt e trên quỹ đạo là:
\(\begin{array}{*{20}{l}}{T = \dfrac{{2\pi r}}{v} = \dfrac{{2\pi .{n^2}.{r_0}}}{{\sqrt {\dfrac{{k.{e^2}}}{{m.{n^2}.{r_0}}}} }} = \dfrac{{2\pi .{n^3}.\sqrt {m.r_0^3} }}{{e.\sqrt k }}}\\{{T_n} = \dfrac{{2\pi .{n^2}.{r_0}}}{{\dfrac{{5a}}{n}}} = \dfrac{{2\pi .{n^3}.{r_0}}}{{5a}} = \dfrac{{2\pi .{n^3}.{r_0}}}{v} = \dfrac{{128.\pi .{r_0}}}{v} = > n = 4}\end{array}\)
\(n = 4\) là quỹ đạo dừng N
Câu hỏi 50 :
Một máy phát sóng điện từ đang phát sóng theo phương thẳng đứng hướng lên. Biết tại điểm M trên phương truyền vào thời điểm t, véctơ cảm ứng từ đang cực đại và hướng về phía Tây. Vào thời điểm t thì véctơ cường độ điện trường đang:
- A
độ lớn bằng không.
- B
độ lớn cực đại và hướng về phía Đông.
- C
độ lớn cực đại và hướng về phía Bắc
- D
độ lớn cực đại và hướng về phía Nam.
Đáp án: C
Phương pháp giải:
+ Vận dụng lí thuyết về phương, chiều của véctơ cường độ điện trường, véctơ cảm ứng từ và vận tốc truyền sóng trong điện từ trường.
+ Áp dụng quy tắc cái đinh ốc
Lời giải chi tiết:
Ta có:
+ $\overrightarrow E ,\overrightarrow v ,\overrightarrow B $ tạo tam diện thuận theo chiều quay từ E đến B thì chiều tiến là chiều v
