Đề bài
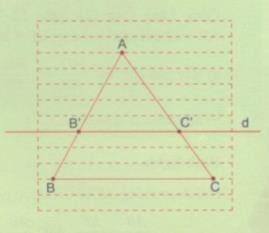
Vẽ tam giác ABC trên giấy kẻ ngang như hình bên. Dựng đường thẳng d song song với BC cắt AB, AC lần lượt tại B’ và C’. Đường thẳng d định ra trên cạnh AB các đoạn thẳng AB’, B’B, AB và định ra trên cạnh AC các đoạn thẳng AC’, C’C, AC
a) Lấy một đoạn chắn trên mỗi cạnh làm đơn vị đo độ dài các đoạn thẳng trên cạnh đó, hãy tính các tỉ số \(\dfrac{{AB'}}{{AB}},{\kern 1pt} {\kern 1pt} \dfrac{{AC'}}{{AC}},{\kern 1pt} {\kern 1pt} \dfrac{{AB'}}{{C'C}},{\kern 1pt} {\kern 1pt} \dfrac{{B'B}}{{AB}},{\kern 1pt} {\kern 1pt} \dfrac{{C'C}}{{AC}}\)
b) So sánh các tỉ số \(\dfrac{{AB'}}{{AB}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \& \dfrac{{AC'}}{{AC}}{\kern 1pt} ,{\kern 1pt} {\kern 1pt} \dfrac{{AB'}}{{B'B}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \& {\kern 1pt} {\kern 1pt} \dfrac{{AC'}}{{C'C}}{\kern 1pt} ,\)\({\kern 1pt} {\kern 1pt} \dfrac{{B'B}}{{AB}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \& \dfrac{{C'C}}{{AC}}.\)
Lời giải chi tiết
a)
\(\eqalign{
& \frac{{AB'}}{{AB}} = \frac{5}{8},\frac{{AC'}}{{AC}} = \frac{5}{8}; \cr
& \frac{{AB'}}{{BB'}} = \frac{5}{3},\frac{{AC'}}{{CC'}} = \frac{5}{3}; \cr
& \frac{{BB'}}{{AB}} = \frac{3}{8},\frac{{CC'}}{{AC}} = \frac{3}{8} \cr} \)
b)
\(\eqalign{
& \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}}\left( { = \frac{5}{8}} \right); \cr
& \frac{{AB'}}{{BB'}} = \frac{{AC'}}{{C'C}}\left( { = \frac{5}{3}} \right); \cr
& \frac{{B'B}}{{AB}} = \frac{{C'C}}{{AC}}\left( { = \frac{3}{8}} \right) \cr} \)
soanvan.me
