Đề bài
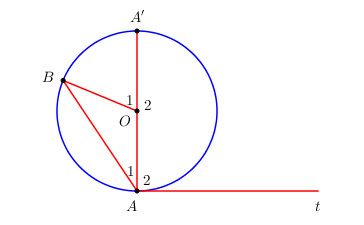
Vẽ cung lớn AB trên đường tròn (O) và tia tiếp tuyến At tiếp xúc với đường tròn sao cho tâm O nằm bên trong góc tù \(\widehat {BAt}\). Vẽ đường kính AA’. Hãy so sánh số đo các cặp góc \(\widehat {{A_1},}\widehat {{O_1}}\) và\(\widehat {{A_2},}\widehat {{O_2}}\). Từ đó so sánh góc \(\widehat {BAt}\) và số đo cung lớn .
Lời giải chi tiết
Ta có:
\(\widehat {{A_1}}\) là góc nội tiếp chắn cung A’B, \(\widehat {{O_1}}\) là góc ở tâm chắn cung \(A'B\)
\( \Rightarrow \widehat {{A_1}} = \dfrac{1}{2}\widehat {{O_1}}\) (góc nội tiếp có số đo bằng nửa số đo góc ở tâm cùng chắn một cung).
Ta có:
\(\widehat {{A_2}} = {90^0}\) (do At là tiếp tuyến của đường tròn (O) tại A).
\(\widehat {{O_2}} = {180^0}\) (do AA’ là đường kính của đường tròn (O) nên O, A, A’ thẳng hàng)
\( \Rightarrow \widehat {{A_2}} = \dfrac{1}{2}\widehat {{O_2}}\).
Ta có: \(\widehat {BAt} = \widehat {{A_1}} + \widehat {{A_2}}\)
Số đo cung lớn AB \( = \widehat {{O_1}} + \widehat {{O_2}}\).
Mà \(\widehat {{A_1}} = \dfrac{1}{2}\widehat {{O_1}};\,\,\widehat {{A_2}} = \dfrac{1}{2}\widehat {{O_2}}\,\,\left( {cmt} \right) \)
\(\Rightarrow \widehat {BAt} = \dfrac{1}{2}\) số đo cung lớn AB.
soanvan.me
