Đề bài
Vật AB đặt trước một thấu kính, vuông góc với trục chính, A nằm trên trục chính. Chiều cao của vật là h=3cm. Tiêu cự của thấu kính là f=12 cm. Khoảng cách từ AB đến thấu kính là d.
a) Dựng ảnh A’B’ trong các trường hợp sau:
- Thấu kính hội tụ, d = 20cm
- Thấu kính hội tụ, d = 8cm
- Thấu kính phân kì, d = 8cm.
b) Ảnh của Ab là ảnh ảo do các trường hợp nào nêu trên ? Dựa vào hình vẽ để so sánh độ lớn của ảnh ảo trong các trường hợp đó.
c) Chọn một trong ba trường hợp nêu ở câu a, dựa vào hình vẽ khi dựng ảnh và dùng các phép tính hình học, hãy tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh.
Lời giải chi tiết
a) Dựng ảnh A’B’ trong các trường hợp
- Thấu kính hội tụ, d = 20cm biểu diễn bởi hình 26.17b.

- Thấu kính hội tụ, d = 8cm biểu diễn bởi hình 26.17c.
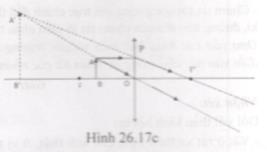
- Thấu kính phân kì, d = 8cm biểu diễn bởi hình 26.17d.
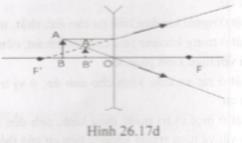
b) Ảnh của AB trong hình 26.17c và hình 26.17d là ảo ảnh.
Trong hình 26.17c ảnh ảo cùng chiều lớn hơn vật. Trong hình 26.17d ảnh ảo cùng chiều nhỏ hơn vật.
c) Tính toán vị trí và độ cao ảnh cho hình 26.17b, với d = 20cm.
Xét \(\Delta ABO \sim \Delta A'B'O\) (góc góc). Ta có: \({{BO} \over {B'O}} = {{AB} \over {A'B'}}\,\,(1)\)
Xét \(\Delta POF' \sim \Delta A'B'F'\) (góc góc). Ta có: \({{PO} \over {A'B'}} = {{OF} \over {B'F}}\,\,\)
Vì PO = AB và B’F’ = B’O – OF’ nên \({{AB} \over {A'B'}} = {{OF} \over {BO' - OF}}\,\,\,\,(2)\)
Từ (1) và (2) ta suy ra: \({{BO} \over {B'O}} = {{OF} \over {B'O - OF}}\) \(\Rightarrow B'O = {{BO.OF} \over {BO - OF}} = {{20.12} \over {20 - 12}} = 30\,\,\left( {cm} \right)\)
Thay lại (2) ta có:
\({3 \over {A'B'}} = {{12} \over {30 - 12}} \Rightarrow A'B' = 4,5\,\,cm\)
Vậy ảnh cách thấu kính 30 cm và cao 4,5 cm.
soanvan.me
