1. Các kiến thức cần nhớ
Tập nghiệm của bất phương trình
+ Số \(x = a\) gọi là nghiệm của một bất phương trình nếu ta thay \(x = a\) vào bất phương trình thì được một bất đẳng thức đúng.
+ Tập hợp tất cả các nghiệm của một bất phương trình gọi là tập nghiệm của bất phương trình. Giải bất phương trình là tìm tập nghiệm của bất phương trình đó.
+Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm
Kí hiệu: "\( \Leftrightarrow \)" đọc là tương đương.
Ví dụ:
+ Hình 1a biểu diễn tập nghiệm của bất phương trình \(x > 2\) .
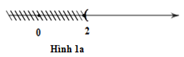
+ Hình 1b biểu diễn tập nghiệm của bất phương trình \(x \le 4\) .
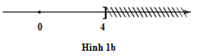
Bất phương trình bậc nhất một ẩn
Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,\) \(ax + b \ge 0,\) \(ax + b \le 0\)) trong đó \(a\) và \(b\) là hai số đã cho, \(a \ne 0\), gọi là bất phương trình bậc nhất một ẩn.
Ví dụ: \(4x + 3 > 0;\,5 - 2x < 2\) là những bất phương trình bậc nhất một ẩn.
Qui tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu hạng tử đó.
Qui tắc nhân với một số:
Khi nhân hai vế của bất phương trình với cùng một số khác $0,$ ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương.
+ Đổi chiều bất phương trình nếu số đó âm.
Ví dụ: \(2x - 5 > 3 \Leftrightarrow 2x > 3 + 5 \)\(\Leftrightarrow 2x > 8\)\( \Leftrightarrow x > 4\)
2. Các dạng toán thường gặp
Dạng 1: Xác định nghiệm, tập nghiệm của bất phương trình và biểu diễn trên trục số
Phương pháp:
Ta sử dụng các quy tắc sau:
* Qui tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu hạng tử đó.
* Qui tắc nhân với một số: Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
+ Giữ nguyên chiều bất phương trình nếu số đó dương;
+ Đổi chiều bất phương trình nếu số đó âm.
Ngoài ra ta còn sử dụng hằng đẳng thức, quy đồng mẫu… để biến đổi.
Dạng 2: Xác định hai bất phương trình tương đương
Phương pháp:
Bất phương trình tương đương: Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.
